题目内容
 如图所示,虚线MN下方存在竖直向上的匀强电场,场强E=2×103V/m,电场区域上方有一竖直放置长为l=0.5m的轻质绝缘细杆,细杆的上下两端分别固定一个带电小球A、B,它们的质量均为m=0.01kg,A带正电,电量为q1=2.5×10-4C;B带负电,电荷量q2=5×10-5C,B到MN的距离h=0.05m.现将轻杆由静止释放(g取10m/s2),求:
如图所示,虚线MN下方存在竖直向上的匀强电场,场强E=2×103V/m,电场区域上方有一竖直放置长为l=0.5m的轻质绝缘细杆,细杆的上下两端分别固定一个带电小球A、B,它们的质量均为m=0.01kg,A带正电,电量为q1=2.5×10-4C;B带负电,电荷量q2=5×10-5C,B到MN的距离h=0.05m.现将轻杆由静止释放(g取10m/s2),求:(1)小球B刚进入匀强电场后的加速度大小.
(2)从开始运动到A刚要进入匀强电场过程的时间.
(3)小球B向下运动离M、N的最大距离.
分析:1、小球B刚进入电场时,以A、B球及轻杆为一整体,运用牛顿第二定律2mg+q2E=2ma,代入数据计算可解得小球B刚进入匀强电场后的加速度大小.
2、分两个阶段研究,第一阶段:B球进入电场前,A、B球及轻杆整体做自由落体运动,则有h=
gt12,代入数据可解得时间t1和B球进入电场瞬间速度v1=gt1.
第二阶段:从B球进入电场到A球刚要进入电场过程,A、B球整体做匀加速运动,则有l=v1t2+
at22,代入数据可解得t2.
所以,从开始运动到A刚要进入匀强电场过程中的时间为t=t1+t2.
3、A、B球整体从开始运动到达最低点过程中,运用动能定理2mg(h+s)+q2Es-q1E(s-l)=0,代入数据可解得小球B向下运动离M、N的最大距离s.
2、分两个阶段研究,第一阶段:B球进入电场前,A、B球及轻杆整体做自由落体运动,则有h=
| 1 |
| 2 |
第二阶段:从B球进入电场到A球刚要进入电场过程,A、B球整体做匀加速运动,则有l=v1t2+
| 1 |
| 2 |
所以,从开始运动到A刚要进入匀强电场过程中的时间为t=t1+t2.
3、A、B球整体从开始运动到达最低点过程中,运用动能定理2mg(h+s)+q2Es-q1E(s-l)=0,代入数据可解得小球B向下运动离M、N的最大距离s.
解答:解:(1)小球B刚进入电场时,以A、B球及轻杆为一整体,做加速度为a的匀加速运动,由牛顿第二定律:
2mg+q2E=2ma
解得a=g+
=15 m/s2
(2)B球进入电场前,A、B球及轻杆整体做自由落体运动,时间为t1,则有h=
gt12
解得:t1=0.1 s
B球进入电场瞬间速度:v1=gt1=1 m/s
从B球进入电场到A球刚要进入电场过程,A、B球整体做匀加速运动,时间为t2,则有l=v1t2+
at22
解方程得:t2=0.2 s
从开始运动到A刚要进入匀强电场过程中的时间
t=t1+t2=0.3 s.
(3)设小球B向下运动离MN最大距离为s,A、B球整体从开始运动到达最低点过程中,由动能定理得:
2mg(h+s)+q2Es-q1E(s-l)=0
解得:s=1.3m.
答:(1)小球B刚进入匀强电场后的加速度大小为15m/s.
(2)从开始运动到A刚要进入匀强电场过程的时间0.3s.
(3)小球B向下运动离M、N的最大距离1.3m.
2mg+q2E=2ma
解得a=g+
| q2E |
| 2m |
(2)B球进入电场前,A、B球及轻杆整体做自由落体运动,时间为t1,则有h=
| 1 |
| 2 |
解得:t1=0.1 s
B球进入电场瞬间速度:v1=gt1=1 m/s
从B球进入电场到A球刚要进入电场过程,A、B球整体做匀加速运动,时间为t2,则有l=v1t2+
| 1 |
| 2 |
解方程得:t2=0.2 s
从开始运动到A刚要进入匀强电场过程中的时间
t=t1+t2=0.3 s.
(3)设小球B向下运动离MN最大距离为s,A、B球整体从开始运动到达最低点过程中,由动能定理得:
2mg(h+s)+q2Es-q1E(s-l)=0
解得:s=1.3m.
答:(1)小球B刚进入匀强电场后的加速度大小为15m/s.
(2)从开始运动到A刚要进入匀强电场过程的时间0.3s.
(3)小球B向下运动离M、N的最大距离1.3m.
点评:本题有一定的难度,要注意受力的变化导致加速度变化,运动过程要分析清楚,分阶段计算,比较好.

练习册系列答案
相关题目
 如图所示,虚线MN左侧的整个空间存在一方向竖直向下的匀强电场E1,虚线右侧的整个空间存在方向竖直向上的匀强电场E2和方向垂直纸面向内的匀强磁场B.一绝缘带电小球从距MN左侧的A点以一定的初速度向右运动,进入虚线右侧后在竖直面内做匀速圆周运动,向左穿过MN后恰好落回A点.已知A点到MN 的距离为L;小球的质量为m、带电量为q,小球的初速度为v0,小球与水平面的动摩擦因数μ=v02/4gL;E1=mg/2q.
如图所示,虚线MN左侧的整个空间存在一方向竖直向下的匀强电场E1,虚线右侧的整个空间存在方向竖直向上的匀强电场E2和方向垂直纸面向内的匀强磁场B.一绝缘带电小球从距MN左侧的A点以一定的初速度向右运动,进入虚线右侧后在竖直面内做匀速圆周运动,向左穿过MN后恰好落回A点.已知A点到MN 的距离为L;小球的质量为m、带电量为q,小球的初速度为v0,小球与水平面的动摩擦因数μ=v02/4gL;E1=mg/2q.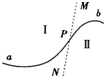 如图所示,虚线MN将平面分成I和Ⅱ两个区域,两个区域都存在与纸面垂直的匀强磁场.一带电粒子仅在磁场力作用下由I区运动到Ⅱ区,弧线aPb为运动过程中的一段轨迹,其中弧aP与弧Pb的弧长之比为2:1,下列判断一定正确的是( )
如图所示,虚线MN将平面分成I和Ⅱ两个区域,两个区域都存在与纸面垂直的匀强磁场.一带电粒子仅在磁场力作用下由I区运动到Ⅱ区,弧线aPb为运动过程中的一段轨迹,其中弧aP与弧Pb的弧长之比为2:1,下列判断一定正确的是( ) 如图所示,虚线MN为电场、磁场的分界线,匀强电场E=103V/m,方向竖直向上,电场线与边界线MN成45°角,匀强磁场垂直纸面向里,磁感应强度B=1T,在电场中有一点A,A点到边界线MN的垂直距离AO=10cm,将比荷为
如图所示,虚线MN为电场、磁场的分界线,匀强电场E=103V/m,方向竖直向上,电场线与边界线MN成45°角,匀强磁场垂直纸面向里,磁感应强度B=1T,在电场中有一点A,A点到边界线MN的垂直距离AO=10cm,将比荷为