题目内容
位于绝缘水平面上的宽度为L=1m的U形金属导轨，左端串接一电阻R=7.5Ω，金属导轨在外力控制下始终以速度v1=2m/s向右匀速运动，导轨电阻不计。如图所示，虚线PQ右侧区域有重直水平面向上的匀强磁场，磁感应强度B=1T。由于导轨足够长，电阻R始终未进入磁场区域。一质量为m=0.1kg，电阻r=0.5Ω，长度也是L的金属棒，自PQ处以水平向右的初速度v2=4m/s滑上金属导轨，金属棒与导轨间动摩擦因数μ=0.2，且运动过程中始终与导轨垂直接触。金属棒滑上导轨后，经t=0.2s，速度恰好与导轨速度相同，此过程中因摩擦产生热量Q=0.08J。之后，金属棒继续运动，当其速度刚好稳定时，金属棒的总位移s=1.74m。重力加速度g=10m/s2，求：
（1）金属棒最终稳定时速度的大小；
（2）当金属棒速度v=3.2m/s时加速度的大小；
（3）自金属棒滑上导轨至刚好稳定时整个电路中消耗的电能。
（1）金属棒最终稳定时速度的大小； （2）当金属棒速度v=3.2m/s时加速度的大小； （3）自金属棒滑上导轨至刚好稳定时整个电路中消耗的电能。（1）金属棒最后匀速运动，设速度为v3
①
②
③
金属棒做匀速运动 
④
可得v3="1.6m/s " ⑤
（2）当金属棒速度v=3.2m/s时，可推出
⑥
由牛顿第二定律
⑦
a=6m/s2 ⑧
（3）设金属棒从滑上导轨到与导轨速度相同的过程中，导轨的位移为s1，棒的位移为s2，
摩擦生
热 
⑨
导轨位移
⑩
金属棒速度由v2减小到v3的过程中位移为s3=s—s2 
（11）
由动能定理
（12）
由功能关系 E=—W安 可得：E电="0.7J " （14分）
① ② ③金属棒做匀速运动 ④可得v3="1.6m/s " ⑤ （2）当金属棒速度v=3.2m/s时，可推出 ⑥由牛顿第二定律 ⑦a=6m/s2 ⑧ （3）设金属棒从滑上导轨到与导轨速度相同的过程中，导轨的位移为s1，棒的位移为s2，摩擦生热 ⑨导轨位移 ⑩金属棒速度由v2减小到v3的过程中位移为s3=s—s2 （11）由动能定理 （12）由功能关系 E=—W安 可得：E电="0.7J " （14分）略
练习册系列答案
相关题目
、长为L的导体棒MN放在导轨上。甲、乙两根相同的绝缘轻质弹簧一端均与导体棒中点固定连接，另一端均被固定，导体棒始终与导轨垂直并保持良好接触，导轨与导体棒的电阻均忽略不计。初始时刻，两弹簧恰好处于自然长度，导体棒具有水平向左的初速度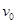
，经过一段时间，导体棒第一次运动至最右端，这一过程中AB间电阻上产生的焦耳热为Q，则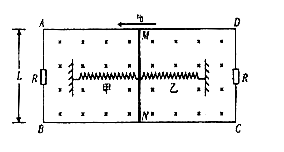
垂直放置在导轨上，金属直杆的电阻是r=0.2Ω，其他电阻忽略不计，金属直杆以一定的初速度v0=4m/s进入磁场，同时受到沿x轴正方向的恒力F=3.5N的作用，在x=6m处速度达到稳定．求：
）金属直杆达到的稳定速度v1是多大？
，设导轨足够长。导轨处在与导轨平面垂直的匀强磁场中，磁感应强度B=0.80T，与导轨上端相连的电源电动势E=4.5V，内阻r=0.4Ω，水平放置的导体棒ab的电阻R=1.5Ω，两端始终与导轨接触良好，且能沿导轨无摩擦滑动，与导轨下端相连的电阻R1=1.0Ω，电路中其它电阻不计。当单刀双掷开关S与1接通时，导体棒刚好保持静止状态，求：
=1m的足够长的平行光滑金属导轨，位于水平的xOy平面内，一端接有阻值为
的电阻．在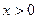
的一侧存在垂直纸面向里的磁场，磁感应强度B只随x的增大而增大，且它们间的关系为B=
x，其中
。一质量为m=0.5kg的金属杆与金属导轨垂直，可在导轨上滑动．当t=0时金属杆位于x=0处，速度为
=
，方向沿x轴的正方向。在运动过程中
沿x轴正方向匀加速直线运动。除电阻R以外其余电阻都可以忽略不计．求：当t=4s时施加于金属杆上的外力为多大。
为水平放置的足够长的平行光滑导轨，导轨间距
，导轨左端连接一个R=2
的电阻，将一根质量
的金属棒
垂直地放置导轨上，且与导轨接触良好，导轨与
金属棒的电阻均不计，整个装置放在磁感强度B=2T的匀强磁场中，磁场方向垂直于导轨平面向下，现对金属棒施加一水平向右的拉力F，并保持拉力的功率恒为P=8W，使棒从静止开始向右运动。已知从金属棒开始运动直至达到稳定速度的过程中电阻R产生的热量
。试解答以下问题：
变化的大致图像。
绕O点在Oxy平面内匀速转动，在它旋转一圈后的过程中（从图示位置开始计时）它的感应电动势与时间的关系图线是图乙中哪一个？ （ ）