题目内容
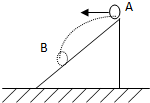如图所示，在一个足够长的斜面上，从A处水平抛出一小球，初动能为3J，落到斜面上B处时的动能为7J，则斜面倾角（ ）| A、30° | B、37° | C、45° | D、60° |
分析：将小球在B点的速度分解，结合动能关系求出竖直分速度与水平分速度之比，根据速度与水平方向的夹角的正切值是位移与水平方向夹角的正切值2倍，得出斜面的倾角大小．
解答：解：小球在B点的动能
mvB2=
mvx2+
mvy2=7J．
小球在A点的动能
mvx2=3J．
则
mvy2=4J
则速度与水平方向的夹角正切值tanα=
=
．
因为tanθ=
=
=
，tanα=
=
．
则tanα=2tanθ
解得：tanθ=
，则斜面的倾角为θ=30°．故A正确，B、C、D错误．
故选：A．
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
小球在A点的动能
| 1 |
| 2 |
则
| 1 |
| 2 |
则速度与水平方向的夹角正切值tanα=
| vy |
| vx |
2
| ||
| 3 |
因为tanθ=
| y |
| x |
| ||
| vxt |
| gt |
| 2vx |
| vy |
| vx |
| gt |
| vx |
则tanα=2tanθ
解得：tanθ=
| ||
| 3 |
故选：A．
点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，知道速度与水平方向的夹角的正切值是位移与水平方向夹角的正切值2倍这一推论．
练习册系列答案
相关题目
如图所示，在一个足够长的斜面上，从A处水平抛出一小球，若抛出时的小球速度为15m/s，g取10m/s2．求：
如图所示，在一个足够大的光滑平面内，有两块质量相同的木块A和B，中间用轻质弹簧连接，用一水平恒力F拉B使A、B和弹簧组成的系统做匀加速直线运动．撤去拉力F后，A、B两物体的运动情况不可能的是（ ）
如图所示，在一个足够大的光滑平面内有A、B两个质量相同的木块，中间用轻质弹簧相连．今对B施以水平瞬时冲量I，此后的运动过程中（ ）