题目内容
 如图所示,在一个足够大的光滑平面内有A、B两个质量相同的木块,中间用轻质弹簧相连.今对B施以水平瞬时冲量I,此后的运动过程中( )
如图所示,在一个足够大的光滑平面内有A、B两个质量相同的木块,中间用轻质弹簧相连.今对B施以水平瞬时冲量I,此后的运动过程中( )分析:分别对A、B进行受力分析,根据牛顿第二定律求解加速度的关系.弹簧伸长到最长时,A、B相对静止,速度相同.弹簧恢复原长时,根据加速度方向与速度方向判断A、B两物体的速度关系.根据系统机械能守恒分析弹簧压缩到最短时系统的总动能.
解答:解:
A、撤去力F后,弹簧的弹力是A物体的合力,也是B物体的合力,A、B质量相等,根据牛顿第二定律得在任意时刻,A、B两物体的加速度大小相等,故A正确.
B、弹簧伸长到最长时,A、B相对静止,速度相同.故B正确.
C、撤去力F后,A加速,B减速,弹簧长度变小,弹簧恢复原长时,A的速度大于B的速度,所以A、B的动量不相等,故C错误.
D、根据系统机械能守恒得弹簧压缩到最短时,弹簧的弹性势能最大,系统的总动能最小,故D错误.
故选:AB.
A、撤去力F后,弹簧的弹力是A物体的合力,也是B物体的合力,A、B质量相等,根据牛顿第二定律得在任意时刻,A、B两物体的加速度大小相等,故A正确.
B、弹簧伸长到最长时,A、B相对静止,速度相同.故B正确.
C、撤去力F后,A加速,B减速,弹簧长度变小,弹簧恢复原长时,A的速度大于B的速度,所以A、B的动量不相等,故C错误.
D、根据系统机械能守恒得弹簧压缩到最短时,弹簧的弹性势能最大,系统的总动能最小,故D错误.
故选:AB.
点评:解决该题关键要能分析A、B两物体的运动情况,知掌握系统机械能守恒的应用,瞬时问题,一般根据牛顿第二定律求解加速度.

练习册系列答案
相关题目
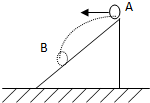 如图所示,在一个足够长的斜面上,从A处水平抛出一小球,初动能为3J,落到斜面上B处时的动能为7J,则斜面倾角( )
如图所示,在一个足够长的斜面上,从A处水平抛出一小球,初动能为3J,落到斜面上B处时的动能为7J,则斜面倾角( )| A、30° | B、37° | C、45° | D、60° |
 如图所示,在一个足够长的斜面上,从A处水平抛出一小球,若抛出时的小球速度为15m/s,g取10m/s2.求:
如图所示,在一个足够长的斜面上,从A处水平抛出一小球,若抛出时的小球速度为15m/s,g取10m/s2.求: 如图所示,在一个足够大的光滑平面内,有两块质量相同的木块A和B,中间用轻质弹簧连接,用一水平恒力F拉B使A、B和弹簧组成的系统做匀加速直线运动.撤去拉力F后,A、B两物体的运动情况不可能的是( )
如图所示,在一个足够大的光滑平面内,有两块质量相同的木块A和B,中间用轻质弹簧连接,用一水平恒力F拉B使A、B和弹簧组成的系统做匀加速直线运动.撤去拉力F后,A、B两物体的运动情况不可能的是( )