题目内容
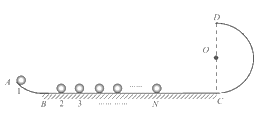
【题目】如图所示,竖直平面内固定一光滑轨道ABCD,分别由弧面AB段、水平面BC段和半圆弧面CD段组成,三段轨道分别在B点和C点平滑连接,已知半圆弧面半径为R,直径DOC垂直BC。大小相同的小球从左到右依次编号为1、2、3……、N,间隔一定距离静止在水平轨道上,已知每个小球的质量为其相邻左边小球质量的k倍(k<1)。将质量为m的1号小球置于弧面AB段高出水平面BC为![]() 的位置,由静止释放,在水平轨道上与2号小球碰撞,2号小球再与3号小球碰撞……。所有碰撞均为对心正碰且无机械能损失,重力加速度为g。求:
的位置,由静止释放,在水平轨道上与2号小球碰撞,2号小球再与3号小球碰撞……。所有碰撞均为对心正碰且无机械能损失,重力加速度为g。求:
(1)1号小球与2号小球碰撞之后,2号小球的速度大小;
(2)当N=3时第3个小球滑上圆轨道后对C点的压力;
(3)为保证N=5时第5个小球在第一次被碰撞后不会脱离半圆轨道,求k的取值范围。
【答案】(1)v2=![]() ;(2)k2mg[
;(2)k2mg[![]() +1];方向竖直向下;(3)
+1];方向竖直向下;(3)![]() k
k![]() 1;或者k
1;或者k![]() -1
-1
【解析】
(1)根据动量守恒定律和机械能守恒求解1号小球与2号小球碰撞之后,2号小球的速度大小;(2)根据动量守恒定律和机械能守恒求解3号小球被碰后的速度,应用牛顿第二定律可得第3个小球滑上圆轨道后对C点的压力;(3)根据小球不脱离轨道的条件以及能经过最高点的条件求解.
(1)设1号碰前的速度为v1,对于1号小球由释放点运动到最低点过程,根据机械能守恒有![]()
设1号、2号小球碰撞后的速度分别为v1′和v2,取水平向右为正方向。
设2号小球的质量为m2,对于1、2号小球碰撞的过程,根据动量守恒定律有
![]()
根据机械能守恒有![]()
解得:![]()
(2)设2号、3号小球碰撞后的速度分别为v2′和v3,对于2、3号小球碰撞的过程,根据动量守恒定律有![]()
根据机械能守恒有![]()
同理可解得:3号小球被碰后的速度![]()
在C点,对3号小球应用牛顿第二定律可得![]()
根据牛顿第三定律3号小球对轨道的压力![]()
方向竖直向下
(3)由(2)中的结果可推知5号小球被碰后的速度![]()
5号小球第一次被碰撞后不会脱离半圆轨道需满足:
情况Ⅰ:![]()
情况Ⅱ:![]()
且在最高点满足:![]()
解得![]()
或者![]()