题目内容
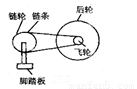
某种变速自行车,有六个飞轮和三个链轮(图1),链轮和飞轮的齿数如下表,前后轮的直径为名称 | 链轮 | 飞轮 |
齿数N/个 | 48 38 28 | 14 16 18 21 24 28 |
C.3.8 rad/s D.7.1 rad/s?

图1
解析:后轮:
后轮![]() ①
①
飞轮:![]() ②
②
由两轮不打滑条件知:
v链=v飞 ③?
有ω链r链=ω飞r飞,
得![]()
至此,需确定轮的半径与齿数间的关系.因圆周长l=2πr,又因每单位长度上的齿数n是一定的,故总齿数为
N=nl=n2πr ⑤
即齿数与半径成正比.找到这一隐含条件对于解决此题至关重要.?
![]() ⑥
⑥
联立以上各式,![]()
式中ω飞=12 rad/s,为使ω链最小,应同时使N飞最小、N链最大.
所以应选择N飞=14 N链=48
![]()
答案:B

 名校课堂系列答案
名校课堂系列答案 某种变速自行车,有六个飞轮和三个链轮,如图所示,链轮和飞轮的齿数如下表所示,前后轮直径为660mm,人骑该车行进速度为4m/s时,脚踩踏板做匀速圆周运动的角速度最小值约为( ) 某种变速自行车,有六个飞轮和三个链轮,如图所示,链轮和飞轮的齿数如下表所示,前后轮直径为660mm,人骑该车行进速度为4m/s时,脚踩踏板做匀速圆周运动的角速度最小值约为( )
| ||||||||||||||||||||
某种变速自行车,有六个飞轮和三个链轮,如图所示,链轮和飞轮的齿数如下表所示,前后轮直径为660mm,人骑该车行进速度为4m/s时,脚踩踏板做匀速圆周运动的角速度最小值约为
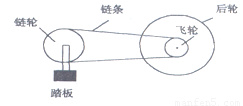
|
名称 |
链轮 |
飞轮 |
|||||||
|
齿数N/个 |
48 |
38 |
28 |
15 |
16 |
18 |
21 |
24 |
28 |
A.1.9rad/s B.3.8rad/s
C.6.5rad/s D.7.1rad/s
 如图所示,某种变速自行车,有六个飞轮和三个链轮,飞轮和链轮的齿数见下表,后轮的直径d=660mm.某人骑该车行进的速度v=4m/s时,脚踩踏板做匀速圆周运动的角速度最小为( )
如图所示,某种变速自行车,有六个飞轮和三个链轮,飞轮和链轮的齿数见下表,后轮的直径d=660mm.某人骑该车行进的速度v=4m/s时,脚踩踏板做匀速圆周运动的角速度最小为( )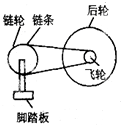 (2011?上海模拟)如图所示,某种变速自行车,有六个飞轮和三个链轮,链轮和飞轮的齿数如下表所示,后轮的直径为d=666mm.当人骑该车,使脚踏板以恒定的角速度转动时,自行车行进的最大速度和最小速度之比为
(2011?上海模拟)如图所示,某种变速自行车,有六个飞轮和三个链轮,链轮和飞轮的齿数如下表所示,后轮的直径为d=666mm.当人骑该车,使脚踏板以恒定的角速度转动时,自行车行进的最大速度和最小速度之比为