题目内容
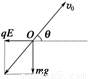
一匀强电场，场强方向是水平的(如图)，一个质量为m的带正电的小球，从O点出发、初速度的大小为v0，在电场力与重力的作用下，恰能沿与电场线成θ角的直线运动．求小球运动到最高点时其电势能与在O点的电势能之差．
【答案】
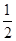mv
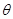cos2θ
【解析】设电场强度为E，小球带电荷量为q，因为小球做直线运动，它所受的电场力qE和重力mg的合力必沿此直线，如图所示，所以mg＝qEtanθ.
由此可知，小球做匀减速运动的加速度大小为a＝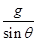
.
设从O点到最高点的位移为L，根据运动学公式有
v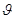
＝2aL
运动的水平位移为x＝Lcosθ.
从O点到最高点的过程中，电场力做负功，电势能增加，小球在最高点与O点的电势能之差为ΔEp＝qEx.
联立以上五式，解得ΔEp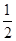＝mv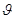cos2θ.
练习册系列答案
相关题目
（2005?辽宁）一匀强电场，场强方向是水平的（如图）．一个质量为m的带正电的小球，从O点出发，初速度的大小为v0，在电场力与重力的作用下，恰能沿与场强的反方向成θ角的直线运动．求小球运动到最高点时其电势能与在O点的电势能之差．
一匀强电场，场强方向是水平的，场强大小未知，如图所示．一个质量为m的带正电的小球，从O点出发，初速度的大小为vo，在电场力和重力的作用下，恰能沿与场强的反方向成θ的直线运动．求：
（2011?抚顺一模）如图所示，直角坐标系在一真空区域里，y轴的左方有一匀强电场，场强方向跟y轴负方向成θ=
在如图所示的空间区域里，y轴左方有一匀强电场，场强方向跟y轴正方向成60°，大小为E=4.0×105N/C；y轴右方有一垂直纸面向里的匀强磁场，磁感应强度B=0.20T．有一质子以速度v=2.0×106m/s，由x轴上的A点（10cm，0）沿与x轴正方向成30°斜向上射入磁场，在磁场中运动一段时间后射入电场，后又回到磁场，经磁场作用后又射入电场．已知质子质量近似为m=1.6×10-27kg，电荷q=1.6×10-19C，质子重力不计．求：
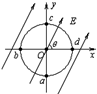如图所示，以O点为圆心，以R=0.20m为半径的圆与坐标轴交点分别为a、b、c、d，该圆所在平面内有一匀强电场，场强方向与x轴正方向成θ=60°角，已知a、b、c 三点的电势分别为4| 3 |
| 3 |
A、该匀强电场的场强E=40
| ||
| B、该匀强电场的场强E=80V/m | ||
C、d点的电势为-2
| ||
| D、d点的电势为-4V |