题目内容
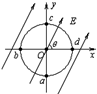 如图所示,以O点为圆心,以R=0.20m为半径的圆与坐标轴交点分别为a、b、c、d,该圆所在平面内有一匀强电场,场强方向与x轴正方向成θ=60°角,已知a、b、c 三点的电势分别为4
如图所示,以O点为圆心,以R=0.20m为半径的圆与坐标轴交点分别为a、b、c、d,该圆所在平面内有一匀强电场,场强方向与x轴正方向成θ=60°角,已知a、b、c 三点的电势分别为4| 3 |
| 3 |
A、该匀强电场的场强E=40
| ||
| B、该匀强电场的场强E=80V/m | ||
C、d点的电势为-2
| ||
| D、d点的电势为-4V |
分析:匀强电场中,电势差与电场强度的关系为U=Ed,d是两点沿电场强度方向的距离,根据此公式和ac间的电势差,求出电场强度E.
由题可知,圆心O点的电势为0,根据U=Ed分析d、b间电势差的关系,即可求得d点的电势.
由题可知,圆心O点的电势为0,根据U=Ed分析d、b间电势差的关系,即可求得d点的电势.
解答:解:由题意得,a、c间的电势差为 Uac=φa-φc=4
V-(-4
V)=8
V.
a、c两点沿电场强度方向的距离为 d=2Rsinθ=2×0.2×
m=
m
故该匀强电场的场强 E=
=
V/m=40V/m.
根据匀强电场中电势差与电场强度的关系式U=Ed,相等距离,电势差相等,因为φa=4
V,φc=-4
V,可知,O点电势为0,而dO=Oa,则a、O间的电势差等于O、a间的电势差,可知,d点的电势为-4V,故ABC错误,D正确.
故选:D
| 3 |
| 3 |
| 3 |
a、c两点沿电场强度方向的距离为 d=2Rsinθ=2×0.2×
| ||
| 2 |
| ||
| 5 |
故该匀强电场的场强 E=
| Uac |
| d |
8
| ||||
|
根据匀强电场中电势差与电场强度的关系式U=Ed,相等距离,电势差相等,因为φa=4
| 3 |
| 3 |
故选:D
点评:解决本题的关键是正确理解U=Ed,分析匀强电场中两点间的电势差关系,并能正确求解场强.

练习册系列答案
相关题目
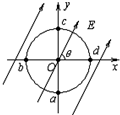 如图所示,以O点为圆心,以R=0.20m为半径的圆与坐标轴交点分别为a、b、c、d,该圆所在平面内有一匀强电场,场强方向与x轴正方向成θ=60°角,已知a、b、c 三点的电势分别为4
如图所示,以O点为圆心,以R=0.20m为半径的圆与坐标轴交点分别为a、b、c、d,该圆所在平面内有一匀强电场,场强方向与x轴正方向成θ=60°角,已知a、b、c 三点的电势分别为4| 3 |
| 3 |
| A、该匀强电场的场强E=40V/m |
| B、该匀强电场的场强E=80V/m |
| C、d点的电势为x=+∞V |
| D、d点的电势为x=-∞V |
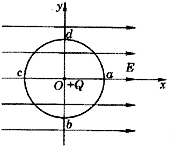 在如图所示,以O点为圆心,以r为半径的圆与坐标轴交点分别为a、b、c、d,空间有一与x轴正方向相同的匀强电场,同时,在O点固定一个电量为+Q的点电荷.如果把一个带电量为-q的检验电荷放在c点,恰好平衡,求:
在如图所示,以O点为圆心,以r为半径的圆与坐标轴交点分别为a、b、c、d,空间有一与x轴正方向相同的匀强电场,同时,在O点固定一个电量为+Q的点电荷.如果把一个带电量为-q的检验电荷放在c点,恰好平衡,求:
 V 、4V、
V 、4V、 V,则下列说法正确的是
V,则下列说法正确的是
 V/m
V/m V
V V
V