题目内容
天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.经观测某双星系统中两颗恒星A、B围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T.已知恒星A、B之间的距离为L,A、B的质量之比2:1,万有引力常量为G,求:
(1)恒星A做匀速圆周运动的轨道半径RA;
(2)双星的总质量M.
(1)恒星A做匀速圆周运动的轨道半径RA;
(2)双星的总质量M.
分析:这是一个双星的问题,两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,它们之间的万有引力提供各自的向心力,两颗恒星有相同的角速度和周期,结合牛顿第二定律和万有引力定律解决问题.
解答:解:(1)如图,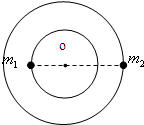
设双星中质量为m1的天体轨道半径为RA,质量为m2的天体轨道半径为RB
据万有引力定律和牛顿第二定律,得:G
=m1ω2RA----①
G
=m2ω2RB----②
RA+RB=L----③
由①②③联立解得:RA=
L=
L=
L
(2)根据万有引力提供向心力:G
=m1(
)2RA 得
则m1+m2=
即双星的总质量M=
答:(1)恒星A做匀速圆周运动的轨道半径RA为
L.
(2)双星的总质量M为
.

设双星中质量为m1的天体轨道半径为RA,质量为m2的天体轨道半径为RB
据万有引力定律和牛顿第二定律,得:G
| m1m2 |
| L2 |
G
| m1m2 |
| L2 |
RA+RB=L----③
由①②③联立解得:RA=
| m2 |
| m1+m2 |
| 1 |
| 2+1 |
| 1 |
| 3 |
(2)根据万有引力提供向心力:G
| m1m2 |
| L2 |
| 2π |
| T |
则m1+m2=
| 4π2L3 |
| GT2 |
即双星的总质量M=
| 4π2L3 |
| GT2 |
答:(1)恒星A做匀速圆周运动的轨道半径RA为
| 1 |
| 3 |
(2)双星的总质量M为
| 4π2L3 |
| GT2 |
点评:本题是双星问题,与卫星绕地球运动模型不同,两颗星都绕同一圆心做匀速圆周运动,关键抓住条件:相同的角速度和周期.

练习册系列答案
相关题目