题目内容
（2008?宁夏）天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星．双星系统在银河系中很普遍．利用双星系统中两颗恒星的运动特征可推算出它们的总质量．已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T，两颗恒星之间的距离为r，试推算这个双星系统的总质量．（引力常量为G）
分析：这是一个双星的问题，两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动，它们之间的万有引力提供各自的向心力，两颗恒星有相同的角速度和周期，结合牛顿第二定律和万有引力定律解决问题．
解答：解：设两颗恒星的质量分别为m1、m2，做圆周运动的半径分别为r1、r2，角速度分别为ω1，ω2．根据题意有
ω1=ω2①
r1+r2=r②
根据万有引力定律和牛顿定律，有
G
=m1
r1③
G
=m2
r2④
联立以上各式解得 r1=
⑤
根据解速度与周期的关系知ω1=ω2=
⑥
联立③⑤⑥式解得m1+m2=
r3⑦
答：这个双星系统的总质量是
r3
ω1=ω2①
r1+r2=r②
根据万有引力定律和牛顿定律，有
G
| m1m2 |
| r2 |
| ω | 2 1 |
G
| m1m2 |
| r2 |
| ω | 2 2 |
联立以上各式解得 r1=
| m2r |
| m1+m2 |
根据解速度与周期的关系知ω1=ω2=
| 2π |
| T |
联立③⑤⑥式解得m1+m2=
| 4π2 |
| T2G |
答：这个双星系统的总质量是
| 4π2 |
| T2G |
点评：本题是双星问题，与卫星绕地球运动模型不同，两颗星都绕同一圆心做匀速圆周运动，关键抓住条件：相同的角速度和周期．
练习册系列答案
相关题目
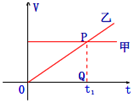（2008?宁夏）甲乙两车在公路上沿同一方向做直线运动，它们的v-t图象如图所示．两图象在t=t1时相交于P点，P在横轴上的投影为Q，△OPQ的面积为S．在t=0时刻，乙车在甲车前面，相距为d．已知此后两车相遇两次，且第一次相遇的时刻为t′，则下面四组t′和d的组合可能是（ ）
（2008?宁夏）一定质量的理想气体被活塞封闭在可导热的气缸内，活塞相对于底部的高度为h，可沿气缸无摩擦地滑动．取一小盒沙子缓慢地倒在活塞的上表面上．沙子倒完时，活塞下降了
（2008?宁夏）一滑块在水平地面上沿直线滑行，t=0时其速度为1m/s．从此刻开始滑块运动方向上再施加一水平面作用F，力F和滑块的速度v随时间的变化规律分别如图a和图b所示．设在第1秒内、第2秒内、第3秒内力F对滑块做的功分别为W1、W2、W3，则以下关系正确的是（ ）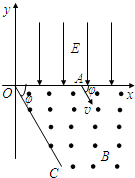
（2008?宁夏）如图所示，在xOy平面的第一象限有一匀强电场，电场的方向平行于y轴向下；在x轴和第四象限的射线OC之间有一匀强磁场，磁感应强度的大小为B，方向垂直于纸面向外．有一质量为m，带有电荷量+q的质点由电场左侧平行于x轴射入电场．质点到达x轴上A点时，速度方向与x轴的夹角为φ，A点与原点O的距离为d．接着，质点进入磁场，并垂直于OC飞离磁场．不计重力影响．若OC与x轴的夹角φ，求：