题目内容
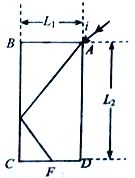
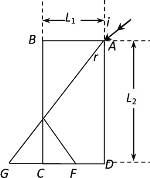
【题目】如图所示，矩形ABCD为某透明介质的截面图，AB边长L1=12cm，BC边长L2=24m，光线由A点以i=53°的入射角射入AB面，光线进入介质后，经过一次反射后，射到底边CD的中点F，并的出个质，不考虑F点光线的反射。已知光速c=3.0×108m/s，sin53°=0.8，cos53°=0.6。求：
(1)介质的折射率
(2)光线在介质中的传播时间。
【答案】（1）
；（2）
s。
【解析】
（1）由几何关系找到光线在A点的折射角，根据折射定律求解折射率；（2）由即可关系求解光在介质中的传播距离，根据
求解时间.
（1）延长A点的折射光线与底边CD交于G点，三角形AGD中，由几何关系可知
GD=
=18cm
AG=
=30cm
由公式 
可得 
（2）在介质中
S=AG=30cm
可得t=s
练习册系列答案
相关题目
