题目内容
(12分).如图所示,长为L的绝缘细线一端悬于O点,另一端系一质量为m、带电荷+q的小球,小球静止时处于O′点。现将此装置放在水平向右的匀强电场中,小球静止在A点时细线与竖直方向成θ角。求:
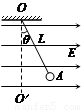
(1)该匀强电场的电场强度大小;
(2)若将小球求从O′点由静止释放,则小球运动到A点时的速度υ多大?
【答案】
(1)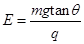 (2)
(2)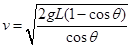
【解析】
试题分析:(1)设电场强度为E,小球受重力mg、电场力qE及线的拉力F。
小球在A点,根据共点力平衡条件有 mgtanθ =qE
解得 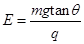
(2)小球从O′点运动到A点的过程中,电场力做正功,重力做负功。设小球到达A点的速度为υ,根据动能定理有
qELsinθ
– mgL ( 1 – cosθ ) =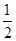 mυ2
mυ2
解得 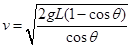
考点:考查了力的平衡条件的应用
点评:力分析时一定要选择合适的研究对象进行正确的受力分析,应用平衡条件进行求解即可.

练习册系列答案
相关题目
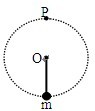 如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周轨道最低点时的速度大小为
如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周轨道最低点时的速度大小为
|
| A、小球不能到达P点 | ||
B、小球到达P点时的速度大于
| ||
| C、小球能到达P点,且在P点受到轻杆向下的拉力 | ||
| D、小球能到达P点,且在P点受到轻杆向上的支持力 |
 (2011?东莞一模)如图所示,长为L的细绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设细绳与竖直方向的夹角为θ.下列说法中正确的是( )
(2011?东莞一模)如图所示,长为L的细绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设细绳与竖直方向的夹角为θ.下列说法中正确的是( )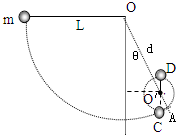 (2009?金山区二模)如图所示,长为L的细绳,一端系有一质量为m的小球,另一端固定在O点.细绳能够承受的最大拉力为7mg.现将小球拉至细绳呈水平位置,然后由静止释放,小球将在竖直平面内摆动.如果在竖直平面内直线OA(OA与竖直方向的夹角为θ)上某一点O′钉一个小钉,为使小球可绕O′点在竖直平面内做圆周运动,且细绳不致被拉断,求:OO′的长度d所允许的范围.
(2009?金山区二模)如图所示,长为L的细绳,一端系有一质量为m的小球,另一端固定在O点.细绳能够承受的最大拉力为7mg.现将小球拉至细绳呈水平位置,然后由静止释放,小球将在竖直平面内摆动.如果在竖直平面内直线OA(OA与竖直方向的夹角为θ)上某一点O′钉一个小钉,为使小球可绕O′点在竖直平面内做圆周运动,且细绳不致被拉断,求:OO′的长度d所允许的范围. 如图所示,长为L的细绳一端固定在O点,另一端系一质量为m的小球.在O点的正下方与O点相距L/2处有一枚光滑小钉,把球拉起使细绳在水平方向伸直,由静止释放.(重力加速度为g)求:
如图所示,长为L的细绳一端固定在O点,另一端系一质量为m的小球.在O点的正下方与O点相距L/2处有一枚光滑小钉,把球拉起使细绳在水平方向伸直,由静止释放.(重力加速度为g)求: 如图所示,长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块,现缓慢地抬高A端,使木板以左端为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动,此时停止转动木板,小物块滑到底端的速度为v,则在整个过程中,下列说法不正确的是( )
如图所示,长为L的长木板水平放置,在木板的A端放置一个质量为m的小物块,现缓慢地抬高A端,使木板以左端为轴转动,当木板转到与水平面的夹角为α时小物块开始滑动,此时停止转动木板,小物块滑到底端的速度为v,则在整个过程中,下列说法不正确的是( )