Question

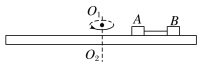
【题目】如图所示，质量为和质量为可视为质点的两物块相距d一起静止在足够长且质量为的木板上，已知、与木板之间的动摩擦因数均为，木板与水平面的动摩擦因数为某时刻同时让、以初速度速度，的速度沿木板向右运动。取，求：

若与不相碰，与间距d的最小值；

在水平面滑行的位移x。

Answer 1

【答案】(1)1.5m；(2)2.5m

【解析】

(1)由牛顿第二定律求出加速度，应用运动学公式求出两质点的位移，然后求出两质点间的初始距离；

(2)由牛顿第二定律求出木板的加速度，然后由运动学公式求出M的位移。

(1) 根据题意知，m1、m2在木板上做减速运动，

M在水平面上做加速运动，由牛顿定律得：

对m1：μ1m1g=m1a1

对m2：μ1m2g=m2a2

对M：μ1m1g+μ1m2g-μ2（m1+m2+M）g=MaM，

设经过t1，M与m2共速且为v，m1的速度为v3，

由运动学公式得：

对m1，速度：v3=v1-a1t1，

位移：

对m2，速度：v=v2-a2t1，

位移：

对M，速度：v=aMt1

位移：

在t1时间内m1与m2的相对位移：△x1=x1-x2，

由题可知M与m2共速后它们相对静止，

其加速度为a，由牛顿第二定律得：

μ1m1g-μ2（m1+m2+M）g=（M+m2）a，

解得：a=0，即：M与m2共速后一起匀速运动，

m1继续减速，设经过t2系统共速，其速度为v′，

由运动学知识，对m1有：v′=v3-a1t2，

位移：

对M和m2整体有：xM′=vt2，△x2=x1′-xM′，

由几何关系可得：d≥△x1+△x2，

代入数据解得：dm=1.5m；

(2) 由题可知系统整体共速后一起减速直到静止，

由牛顿定律得：μ2(m1+m2+M)g＝(M+m1+m2)a′，

由运动学知识得：

M运动的位移为：x=xM+xM′+xM″，

代入数据解得：x=2.5m。