题目内容
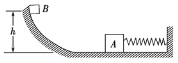
【题目】娱乐场有一种刺激的娱乐活动,装置的简化模型如图所示,在光滑的水平面上停放着一辆质量为![]() 的平板车C,其右端固定一弹性缓冲装置,平板车上表面Q点到小车左端粗糙,Q点到小车右端光滑,且粗糙段长为
的平板车C,其右端固定一弹性缓冲装置,平板车上表面Q点到小车左端粗糙,Q点到小车右端光滑,且粗糙段长为![]() 。小车的左端紧靠着一个固定在竖直平面半径为
。小车的左端紧靠着一个固定在竖直平面半径为![]() 的四分之一光滑圆弧形轨道,轨道底端的切线水平且与小车的上表面相平。现有质量为
的四分之一光滑圆弧形轨道,轨道底端的切线水平且与小车的上表面相平。现有质量为![]() 的物体B放于小车左端,A物体(活动者与滑车)从四分之一圆形轨道顶端P点由静止滑下,A的总质量
的物体B放于小车左端,A物体(活动者与滑车)从四分之一圆形轨道顶端P点由静止滑下,A的总质量![]() 。A滑行到车上立即和物体B结合在一起(结合时间极短),沿平板车向右滑动,一段时间后与平板车达到相对静止,此时他们距Q点距离
。A滑行到车上立即和物体B结合在一起(结合时间极短),沿平板车向右滑动,一段时间后与平板车达到相对静止,此时他们距Q点距离![]() 。已知A和B与小车之间的动摩擦因数相同,重力加速度为
。已知A和B与小车之间的动摩擦因数相同,重力加速度为![]() ,A、B均可视为质点。求:
,A、B均可视为质点。求:
(1)活动者滑到圆弧轨道最低点时对轨道的压力;
(2)物体B与小车之间的动摩擦因数。

【答案】(1)![]() ,方向竖直向下;(2)0.75或者0.25
,方向竖直向下;(2)0.75或者0.25
【解析】
(1)A在圆弧轨道上滑到最低点,设速度为![]() ,由动能定理
,由动能定理
![]()
设此时A受到的支持力为![]()
![]()
解得
![]()
由牛顿第三定律得A对轨道的压力大小为![]() ,方向竖直向下。
,方向竖直向下。
(2)设A、B在一起速度为![]() ,A、B、C三者共同运动的速度为
,A、B、C三者共同运动的速度为![]() ,取
,取![]() 为系统,选取水平向右为正,根据动量守恒定律
为系统,选取水平向右为正,根据动量守恒定律
![]()
取![]() 为系统,动量守恒
为系统,动量守恒
![]()
AB在C上滑动的过程中,设摩擦生热量为Q,由能量守恒得
![]()
解得
![]()
①当![]() 没有滑进光滑段,相对小车的路程为
没有滑进光滑段,相对小车的路程为![]() ,由功能关系得
,由功能关系得
![]()
解得
![]()
②当![]() 滑进光滑段又反弹回到粗糙段,相对小车的路程为
滑进光滑段又反弹回到粗糙段,相对小车的路程为![]() ,由功能关系得
,由功能关系得
![]()
解得
![]()
即粗糙段的动摩擦因数有两种情况,0.75或者0.25。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目