题目内容
5.如图所示,可视为质点的物体A叠放在长木板B上,A、B的质量分别为1=10kg,m2=10kg,B长为L=16cm,开始时A在B的最右端,A与B、B与地之间的动摩擦因数分别为μ1=0.4,μ2=0.4,现将一水平恒力F=200N作用在B上,使A、B由静止开始运动,当A恰好运动到B的中点时撤去外力F,g取10m/s2,求:
(1)力F作用的时间,及此时B前进的距离;
(2)撤去外力F后B还能走多远?
分析 (1)根据牛顿第二定律分别求出A、B在F作用时的加速度,根据位移之差等于$\frac{L}{2}$,求出F作用的时间,根据位移时间公式求出B的位移.
(2)撤去外力F后,根据牛顿第二定律求出A、B的加速度,求出A、B速度相等的时间,求出此过程中的位移,速度相等后,一起做匀减速运动,根据速度位移公式求出匀减速运动的位移,从而得出B还能滑行的位移.
解答 解:(1)力F开始作用时,设A、B的加速度分别为a1、a2,
对A,根据牛顿第二定律得,μ1m1g=m1a1,
代入数据解得a1=4m/s2
对B,根据牛顿第二定律得,F-μm1g-μ2(m1+m2)g=m2a2
代入数据解得a2=8m/s2
设力F作用的时间为t,对应此时A、B的速度为vA、vB
则有$\frac{1}{2}{a}_{2}{t}^{2}-\frac{1}{2}{a}_{1}{t}^{2}=0.08$,
代入数据得,t=0.2s
vA=0.8m/s,vB=1.6m/s
此时B前进的距离为${x}_{B}=\frac{1}{2}{a}_{2}{t}^{2}$=$\frac{1}{2}×8×0.04$m=0.16m=16cm,
(2)力F撤去后,对A有,μ1m1g=m1a3,
代入数据解得a3=4 m/s2
对B有 μ1m1g+μ2(m1+m2)g=m2a4,
代入数据解得a4=12 m/s2,
设A、B经过时间t1达到共同速度v1
则有:vA+a3t1=vB-a4t1,
代入数据解得t1=0.05s v1=1.0m/s
此过程中B前进的距离为${x}_{1}=\frac{{{v}_{B}}^{2}-{{v}_{1}}^{2}}{2{a}_{4}}$,代入数据解得 x1=0.065m=6.5cm
A、B共速后一起匀减速的加速度为a5
μ2(m1+m2)g=(m1+m2)a5,
代入数据解得 a5=4m/s2
此时B前进的距离为${x}_{2}=\frac{{{v}_{1}}^{2}}{2{a}_{5}}$,
代入数据解得 x2=12.5cm
撤去F后B前进的总距离为 x=x1+x2=6.5+12.5cm=19cm
答:(1)力F作用的时间为0.2s,B前进的距离为16cm;
(2)撤去外力F后B还能走19cm.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,关键理清A、B在整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解,难度较大.

 学习实践园地系列答案
学习实践园地系列答案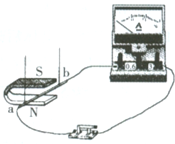 李明利用如图所示实验装置探究电磁感应现象,他把装置中的直铜线ab通过导线接在量程为3A的电流表的两接线柱上,当让ab迅速向右运动时,并未发现电流表指针明显偏转.你认为最可能的原因是( )
李明利用如图所示实验装置探究电磁感应现象,他把装置中的直铜线ab通过导线接在量程为3A的电流表的两接线柱上,当让ab迅速向右运动时,并未发现电流表指针明显偏转.你认为最可能的原因是( )| A. | 感应电流太小,无法使指针明显偏转 | |
| B. | 铜线ab太细,换用铜棒进行实验便能使指针明显偏转 | |
| C. | ab运动方向不对,应将ab改为向左运动 | |
| D. | ab运动方向不对,应将ab改为上下运动 |
| A. | 天体A、B的密度一定相等 | |
| B. | 天体A、B的质量一定相等 | |
| C. | 两颗卫星的线速度一定相等 | |
| D. | 天体A、B表面上物体的重力加速度与天体的半径成正比 |
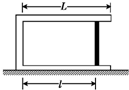 长L=1m的汽缸固定在水平面上,汽缸中有横截面积S=100cm2的光滑活塞,活塞封闭了一定质量的理想气体.当温度t=27℃,大气压p0=1×105Pa时,气柱长度l=90cm,汽缸和活塞的厚度均可忽略不计.
长L=1m的汽缸固定在水平面上,汽缸中有横截面积S=100cm2的光滑活塞,活塞封闭了一定质量的理想气体.当温度t=27℃,大气压p0=1×105Pa时,气柱长度l=90cm,汽缸和活塞的厚度均可忽略不计.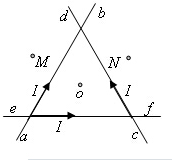 如图所示三根彼此绝缘的无限长直导线的一部分ab,cd,ef构成一个等边三角形,O为三角形的中心,M,N分别为O关于导线ab,cd的对称点,当三根导线中通以大小相等,方向如图的电流时,O点的磁感应强度大小为B1,M点磁感应强度的大小为B2.若将导线ef中的电流撤去,二保持另两根导线中的电流不变,则N点的磁感应强度大小为$\frac{1}{2}$(3B1-B2).
如图所示三根彼此绝缘的无限长直导线的一部分ab,cd,ef构成一个等边三角形,O为三角形的中心,M,N分别为O关于导线ab,cd的对称点,当三根导线中通以大小相等,方向如图的电流时,O点的磁感应强度大小为B1,M点磁感应强度的大小为B2.若将导线ef中的电流撤去,二保持另两根导线中的电流不变,则N点的磁感应强度大小为$\frac{1}{2}$(3B1-B2).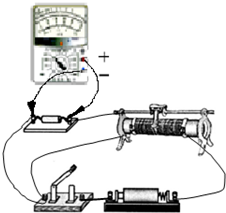 某同学用多用表测量某定值电阻的阻值.
某同学用多用表测量某定值电阻的阻值.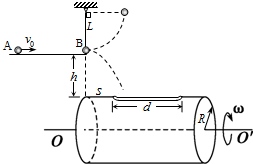 如图所示,小球A以初速v0沿光滑平台向右运动,竖直静止悬挂的小球B,恰好与平台右端接触.一水平放置、半径R=0.5m的薄壁圆桶绕轴OO′匀速转动,转动角速度ω=5πrad/s,桶壁上离左端s=0.2m处开有一长度d=0.8m的长孔,孔宽略大于小球A的直径.圆桶左端和平台右端平齐,顶端距平台h=0.8m.若A、B两球发生弹性正碰时(碰撞时间极短),长孔恰好运动到桶的正上方,碰后B上摆,A沿水平方向抛射向长孔.已知v0方向、悬线和圆桶的轴线在同一竖直面上,小球B的质量为m,A的质量是B的k倍,悬线长L=0.8m,视两球为质点,g=10m/s2,不考虑空气阻力.
如图所示,小球A以初速v0沿光滑平台向右运动,竖直静止悬挂的小球B,恰好与平台右端接触.一水平放置、半径R=0.5m的薄壁圆桶绕轴OO′匀速转动,转动角速度ω=5πrad/s,桶壁上离左端s=0.2m处开有一长度d=0.8m的长孔,孔宽略大于小球A的直径.圆桶左端和平台右端平齐,顶端距平台h=0.8m.若A、B两球发生弹性正碰时(碰撞时间极短),长孔恰好运动到桶的正上方,碰后B上摆,A沿水平方向抛射向长孔.已知v0方向、悬线和圆桶的轴线在同一竖直面上,小球B的质量为m,A的质量是B的k倍,悬线长L=0.8m,视两球为质点,g=10m/s2,不考虑空气阻力.