题目内容
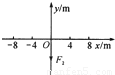
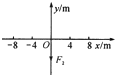 质量M=2kg的质点停在如图所示的平面直角坐标系原点O,当其受到三个同平面的作用力F1、F2、F3时正好在O点处于静止状态.已知三个力中的F2=4N,方向指向y轴的负方向.求:
质量M=2kg的质点停在如图所示的平面直角坐标系原点O,当其受到三个同平面的作用力F1、F2、F3时正好在O点处于静止状态.已知三个力中的F2=4N,方向指向y轴的负方向.求:(1)当停止F2作用时,质点受到的合力大小和方向?
(2)从t=0(质点静止在坐标原点O处)时起,停止其中F1的作用并恢复F2的作用,到第4s末质点位置的坐标是(-8,0),则F1大小和方向如何?
(3)若从第4s末起恢复F1的作用,而同时停止F2作用,则到第6s末质点的位置坐标是多少?第6s末质点的速度大小和方向如何?
分析:(1)三力平衡时,任意两个力的合力与第三个力等值、反向、共线;
(2)停止其中F1的作用并恢复F2的作用,合力与F1等值、反向、共线;物体做匀加速直线运动,故合力向+x方向;根据位移时间关系公式求解出加速度,然后根据牛顿第二定律求解合力;
(3)恢复F1的作用,而同时停止F2作用,合力与F2等值、反向、共线;物体做类似平抛运动;先根据牛顿第二定律求解加速度,然后根据运动学公式求解y方向的分速度,最后得到合速度.
(2)停止其中F1的作用并恢复F2的作用,合力与F1等值、反向、共线;物体做匀加速直线运动,故合力向+x方向;根据位移时间关系公式求解出加速度,然后根据牛顿第二定律求解合力;
(3)恢复F1的作用,而同时停止F2作用,合力与F2等值、反向、共线;物体做类似平抛运动;先根据牛顿第二定律求解加速度,然后根据运动学公式求解y方向的分速度,最后得到合速度.
解答:解:(1)当停止F2的作用时,质点受到的合力大小等于 F2=4N,方向沿y轴的正方向.
(2)停止F1的作用后,F2、F3的合力与F1等值反向,由第4 s末质点的位置坐标(-8,O)知,质点沿x轴负方向做匀加速运动,且S=
a1t2,解得a1=
=
m/s2=1m/s2
故F1=Ma1=2×1N=2N,方向沿x轴正方向;
(3)F1、F3同时作用而F2停止作用时,合力沿y轴正方向大小为4 N,质点做类平抛运动在y轴方向上,则
a2=
=2m/s2,y=
a2
=4m.
在x轴方向上在4s末速度为
Vx=a1tl=1×4 m/s=4m/s
故△x=Vx?t2=4×2 m=8 m
x2=-16 m,y=4m
第6s末的位置坐标(-16,4)
第6 s末时,Vx=4 m/s,Vy=a2t2=4 m/s
故第6秒末时,速度V=
=4
m/s
速度方向指向第三象限,与y轴夹角为450.
答:(1)当停止F2作用时,质点受到的合力大小为4N,方向沿y轴的正方向;
(2)则F1大小为2N,方向沿x轴正方向;
(3)到第6s末质点的位置坐标是为(-16,4),第6s末质点的速度大小为4
m/s,方向与y轴夹角为450
(2)停止F1的作用后,F2、F3的合力与F1等值反向,由第4 s末质点的位置坐标(-8,O)知,质点沿x轴负方向做匀加速运动,且S=
| 1 |
| 2 |
| 2S1 | ||
|
| 2×8 |
| 42 |
故F1=Ma1=2×1N=2N,方向沿x轴正方向;
(3)F1、F3同时作用而F2停止作用时,合力沿y轴正方向大小为4 N,质点做类平抛运动在y轴方向上,则
a2=
| F2 |
| M |
| 1 |
| 2 |
| t | 2 2 |
在x轴方向上在4s末速度为
Vx=a1tl=1×4 m/s=4m/s
故△x=Vx?t2=4×2 m=8 m
x2=-16 m,y=4m
第6s末的位置坐标(-16,4)
第6 s末时,Vx=4 m/s,Vy=a2t2=4 m/s
故第6秒末时,速度V=
|
| 2 |
速度方向指向第三象限,与y轴夹角为450.
答:(1)当停止F2作用时,质点受到的合力大小为4N,方向沿y轴的正方向;
(2)则F1大小为2N,方向沿x轴正方向;
(3)到第6s末质点的位置坐标是为(-16,4),第6s末质点的速度大小为4
| 2 |
点评:本题关键明确物体各个方向上的运动规律,根据受力情况确定加速度,再根据运动学公式列式求解.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
质量m=2kg的质点静止于光滑水平面上,从t=0时刻起,第1s内受到4N的水平外力作用,第2s内受到同方向的2N的外力作用,下列判断正确的是( )
| A、第2s末外力的瞬时功率最大 | ||
| B、0~2 s内外力的平均功率是4.5 W | ||
| C、第2s内外力所做的功是9J | ||
D、第1s内与第2s内质点动能增加量的比值是
|
 质量M=2kg的质点停在如图所示的平面直角坐标系原点O,当其受到三个同平面的作用力F1、F2、F3时正好在O点处于静止状态.已知三个力中的F2=4N.方向指向y轴的负方向.求:
质量M=2kg的质点停在如图所示的平面直角坐标系原点O,当其受到三个同平面的作用力F1、F2、F3时正好在O点处于静止状态.已知三个力中的F2=4N.方向指向y轴的负方向.求: