题目内容
【题目】如图所示,四分之三圆弧形轨道的圆心为O、半径为R,其AC部分粗糙,CD部分光滑,B为最低点,D为最高点.现在A点正上方高为h的P点处由静止释放一质量为m的滑块(可视为质点),滑块从A点处沿切线方向进入圆弧轨道,已知滑块与AC部分轨道间的动摩擦因数处处相等,经过AC部分轨道克服摩擦力做的功为kmgh(k为常数),重力加速度为g,则下列说法中正确的是( )
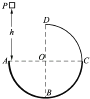
A. 若k=1,则滑块最终将停在B点
B. 滑块经过BC部分轨道克服摩擦力做的功小于![]()
C. 当h=![]() 时,滑块能到达D点
时,滑块能到达D点
D. 当h=![]() 时,滑块能到达D点
时,滑块能到达D点
【答案】BC
【解析】
A、 从P点到C点,由动能定理可得:![]() ,当k=1时,可解得:
,当k=1时,可解得:![]() ,即滑块将在AC之间来回滑动,由于摩擦力做功,机械能减少,最后速度将减为0,受力平衡,有可能停在B点,也有可能停在AB或BC之间的某个位置,故A错误;
,即滑块将在AC之间来回滑动,由于摩擦力做功,机械能减少,最后速度将减为0,受力平衡,有可能停在B点,也有可能停在AB或BC之间的某个位置,故A错误;
B、从A到C,由于摩擦力做功,机械能减少,速率逐渐减小,所需向心力减小,则滑块和轨道之间的正压力减小,而滑动摩擦力等于滑动摩擦因数乘以正压力,所以滑块经过BC部分轨道克服摩擦力做的功小于![]() ,故B正确;
,故B正确;
CD、如果滑块能滑到D点,其最小速度由牛顿第二定律可得:![]() ,从P点到D点,由动能定理可得:
,从P点到D点,由动能定理可得:![]() ,联立解得:
,联立解得:![]() ,故C正确,D错误。
,故C正确,D错误。
故选BC。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目