Question

【题目】如图甲所示，倾角θ=30°的光滑斜面足够长，一轻质弹簧下端与斜面底部的挡板固 定，A、B两木块叠放在轻弹簧上端，且静止在斜面上．已知木块A、B质量分别为0．84 kg和 0．80 kg，弹簧的劲度系数k=100 N/m，若在木块A上施加一个平行于斜面向上的力F，使 A由静止开始以0．25 m/s2的加速度沿斜面向上做匀加速运动．以木块A的的初位置为坐标原点，沿斜面向上建立x轴，力F与木块A沿斜面向上运动的位移x的关系如图乙所示．（g=10 m/s2）求：

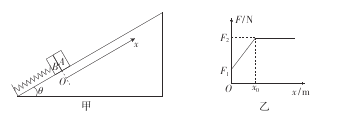
（1）开始时弹簧压缩量x1；

（2）图乙中x0、F1和F2的值；

（3）木块A、B由静止开始匀加速运动到恰好分离的过程中，弹簧的弹性势能变化量．

Answer 1

【答案】（1）8．2×10-2m（2）F1=0．41N； F2=4．41N（3）-0．248J

【解析】

试题分析：（1）对AB整体初始位置由平衡关系可得：（mA+mB）gsinθ=kx1

代入数据可知：x1=8．2×10-2m

（2）AB恰要分离时，对A由牛顿第二定律：F2-mAgsinθ=mAa

代入数据可得：F2=4．41N

对AB整体由牛顿第二定律可知：F2+kx-（mA+mB）gsinθ=（mA+mB）a

代入数据解得：x1=4．2×10-2m

x0=x1-x=4．0×10-2m

AB刚开始运动时，F1+kx1-（mA+mB）gsinθ=（mA+mB）a

代入数据解得：F1=0．41N

（3）对AB由静止开始到分离由动能定理：

由运动学知道：分离时v2=2ax0

代入数据可知：