题目内容
如图所示,一平行板电容器水平放置,两板有方向竖直向上的匀强电场,板间距d=0.40m,电压U=10V,金属板M上开有一小孔。有A、B两个质量均为m=0.10g、电荷量均为q=+8.0×10-5C的带电小球(可视为质点),其间用长为L=0.10m的绝缘轻杆相连,处于竖直状态,A小球恰好位于小孔正上方H=0.20m处。现由静止释放并让两个带电小球保持竖直下落,(g取10m/s2)
求小题1:小球在运动过程中的最大速率。
小题2:小球在运动过程中距N板的最小距离。
求小题1:小球在运动过程中的最大速率。
小题2:小球在运动过程中距N板的最小距离。

小题1:
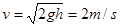
小题2:
(1)由受力分析可知,当F合=0时,速度最大。设有n个球进入电场时,合力为零。
2mg="nEq " 2分
E=U/d
代入数据,n="1"
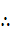 当A球刚进入电场时,F合=0时有V的最大值
当A球刚进入电场时,F合=0时有V的最大值
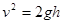 2分
2分
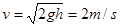 1分
1分
(2) 设B球进入电场x时小球的速度变为0,则根据动能定理有
 3分
3分
解得X=0.2m
A球距N板的最小距离为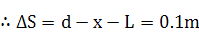 2分
2分
2mg="nEq " 2分
E=U/d
代入数据,n="1"
 当A球刚进入电场时,F合=0时有V的最大值
当A球刚进入电场时,F合=0时有V的最大值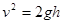 2分
2分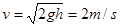 1分
1分(2) 设B球进入电场x时小球的速度变为0,则根据动能定理有
 3分
3分解得X=0.2m
A球距N板的最小距离为
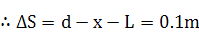 2分
2分
练习册系列答案
相关题目
 ,则下列说法中正确的有
,则下列说法中正确的有 
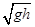





 B两金属板间的电压的大小U;
B两金属板间的电压的大小U; ,将质量为m=1.6×10-6kg、带电量q=3.2×10-8C的微粒以初速度v0=0.5m/s沿两板中线水平射入板间。当滑动变阻器接入电路的阻值为15Ω时,微粒恰好沿中线匀速运动,通过电动机的电流为0.5A。已知电动机内阻R1=2Ω,取g=10m/s2。试问:
,将质量为m=1.6×10-6kg、带电量q=3.2×10-8C的微粒以初速度v0=0.5m/s沿两板中线水平射入板间。当滑动变阻器接入电路的阻值为15Ω时,微粒恰好沿中线匀速运动,通过电动机的电流为0.5A。已知电动机内阻R1=2Ω,取g=10m/s2。试问:
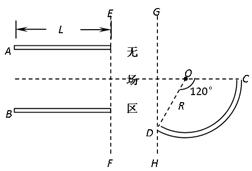
 q的带正电粒子以初速度v0沿两板间的中心线射入匀强电场,粒子出匀强电场经无场区后恰能进入细圆管,并作与管壁无相互挤压的匀速圆周运动。(不计粒子的重力、管的粗细)求:
q的带正电粒子以初速度v0沿两板间的中心线射入匀强电场,粒子出匀强电场经无场区后恰能进入细圆管,并作与管壁无相互挤压的匀速圆周运动。(不计粒子的重力、管的粗细)求: