题目内容
民用航空客机的机舱,一般都设有紧急出口.发生意外情况的飞机在着陆后,打开紧急出口的舱门,会自动生成一个由气囊构成的斜面,机舱中的人可沿该斜面滑行到地面上来.若机舱离气囊底端的竖直高度为h=3.2m,气囊所构成的斜面长度为l=4.0m.一个质量为m=60kg的人在气囊上滑下时所受的阻力为f=240N,则他从机舱滑至底端需多长时间?
分析:人在气囊上滑下时受到的摩擦力为f=μmgcosα,由题,sinθ=
=0.8,cosθ=0.6.根据牛顿第二定律求出加速度,由位移公式x=
at2求出人滑至气囊底端的时间.
| h |
| l |
| 1 |
| 2 |
解答:解:人受力如图所示.
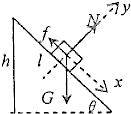
沿斜面方向和垂直于斜面方向建立直角坐标系,设斜面倾角为θ.则sinθ=
=0.8,cosθ=0.6
人在气囊上滑下时受到的摩擦力为 f=μmgcosθ.
根据牛顿第二定律得:mgsinθ-f=ma
解得a=4m/s2
由l=
at2 得t=
s=1.41s
答:他从机舱滑至底端需1.41s的时间.

沿斜面方向和垂直于斜面方向建立直角坐标系,设斜面倾角为θ.则sinθ=
| h |
| l |
人在气囊上滑下时受到的摩擦力为 f=μmgcosθ.
根据牛顿第二定律得:mgsinθ-f=ma
解得a=4m/s2
由l=
| 1 |
| 2 |
| 2 |
答:他从机舱滑至底端需1.41s的时间.
点评:本题知道人的受力情况,根据牛顿第二定律和运动学公式结合研究人运动的时间.基础题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 (2007?铜山县模拟)民用航空客机的机舱一般都设有紧急出口,飞机发生意外情况着陆后,打开紧急出口的舱门,会自动生成一个由气囊构成的斜面.如图所示为某气囊斜面,机舱离底端的竖直高度AB=3.0m,斜面长AC=5.0m,斜面与水平地面CD段间有一段小圆弧平滑连接.乘客与气囊、地面间的动摩擦因数均为μ=0.55,不计空气阻力,g=10m/s2.当乘客从气囊上由静止开始滑到斜面底端C时的速度大小为
(2007?铜山县模拟)民用航空客机的机舱一般都设有紧急出口,飞机发生意外情况着陆后,打开紧急出口的舱门,会自动生成一个由气囊构成的斜面.如图所示为某气囊斜面,机舱离底端的竖直高度AB=3.0m,斜面长AC=5.0m,斜面与水平地面CD段间有一段小圆弧平滑连接.乘客与气囊、地面间的动摩擦因数均为μ=0.55,不计空气阻力,g=10m/s2.当乘客从气囊上由静止开始滑到斜面底端C时的速度大小为