题目内容
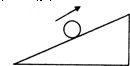
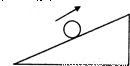
如图所示，有一光滑斜面倾角为θ，放在水平面上，用固定的竖直挡板与斜面夹住一个光滑球，球质量为n．若要使球对竖直挡板无压力，球连同斜面应一起
- A.水平向右加速，加速度a=gtanθ
- B.水平向左加速，加速度a=gtanθ
- C.水平向右减速，加速度a=gsinθ
- D.水平向左减速，加速度a=gsinθ
B
分析：当小球与竖直挡板无压力时，小球受重力和斜面的支持力，与斜面具有共同的加速度，根据小球的受力判断出加速度的方向，从而根据平行四边形定则求出合力的大小，再根据牛顿第二定律求出加速度的大小．
解答：小球受重力和斜面的支持力，根据受力，知道两个力的合力方向水平向左，所以整体的加速度方向水平向左．
根据平行四边形定则，F合=mgtanθ，则a=
．故B正确，A、C、D错误．
故选B．
点评：解决本题的关键知道球与斜面具有共同的加速度，通过隔离对球分析，运用牛顿第二定律得出斜面的加速度．
分析：当小球与竖直挡板无压力时，小球受重力和斜面的支持力，与斜面具有共同的加速度，根据小球的受力判断出加速度的方向，从而根据平行四边形定则求出合力的大小，再根据牛顿第二定律求出加速度的大小．
解答：小球受重力和斜面的支持力，根据受力，知道两个力的合力方向水平向左，所以整体的加速度方向水平向左．
根据平行四边形定则，F合=mgtanθ，则a=
．故B正确，A、C、D错误．故选B．
点评：解决本题的关键知道球与斜面具有共同的加速度，通过隔离对球分析，运用牛顿第二定律得出斜面的加速度．
练习册系列答案
相关题目
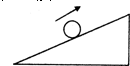如图所示，在一光滑斜面上，有一小球以V0=5m/s 沿斜面向上运动，经2s到达最高点，然后又沿斜面下滑，经3s到达斜面底端，已知小球在斜面上运动的加速度恒定，试求：
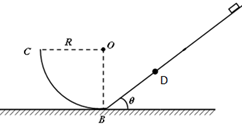如图所示，有一倾角θ=37°的足够长粗糙斜面，底端与一个光滑的
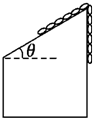如图所示，有一条长为L的均匀金属链条，一半长度在光滑斜面上，斜面倾角为θ，另一半长度沿竖直方向下垂在空中，当链条从静止开始释放后链条滑动，求链条刚好全部滑出斜面时的速度是多大．
