题目内容
2. 如图所示,平行金属导轨AGT和DEF足够长,导轨宽度L=2.0m,电阻不计,AG和DE部分水平、粗糙;GT和EF部分光滑、倾斜,倾角θ=53°,整个空间存在垂直斜面向上的匀强磁场,磁感应强度B=1.0T.金属杆M质量m1=2.0kg,电阻R1=lΩ,轻弹簧K一端固定于O点,O点在bb′中点的正上方,另一端系于金属杆M的中点,轻弹簧劲度系数k=30N/m,金属杆M初始在图中aa′位置静止,弹簧伸长量△l=0.2m,与水平方向夹角a=60°,ab=bc=a′b′=b′c′.另一质量 m2=1.0kg,电阻R2=2的金属杆P从导轨GT和EF上的ss′位置静止释放,后来金属杆M开始滑动,金属杆P从开始下滑x=3.0m达到平衡状态,此时金属杆M刚好到达cc′位置静止,已知重力加速度g=10m/s2,求:
如图所示,平行金属导轨AGT和DEF足够长,导轨宽度L=2.0m,电阻不计,AG和DE部分水平、粗糙;GT和EF部分光滑、倾斜,倾角θ=53°,整个空间存在垂直斜面向上的匀强磁场,磁感应强度B=1.0T.金属杆M质量m1=2.0kg,电阻R1=lΩ,轻弹簧K一端固定于O点,O点在bb′中点的正上方,另一端系于金属杆M的中点,轻弹簧劲度系数k=30N/m,金属杆M初始在图中aa′位置静止,弹簧伸长量△l=0.2m,与水平方向夹角a=60°,ab=bc=a′b′=b′c′.另一质量 m2=1.0kg,电阻R2=2的金属杆P从导轨GT和EF上的ss′位置静止释放,后来金属杆M开始滑动,金属杆P从开始下滑x=3.0m达到平衡状态,此时金属杆M刚好到达cc′位置静止,已知重力加速度g=10m/s2,求:(1)金属杆P的最终速度大小;
(2)金属杆M在cc′位置静止时所受的摩擦力;
(3)从金属杆P开始运动到达到平衡状态的过程中,若金属杆M克服摩擦力做功Wf=2J则金属杆P上产生的热量是多少.
分析 (1)金属杆P从开始下滑x=3.0m达到平衡状态,有牛顿第二定律结合法拉第电磁感应定律和安培力公式求解
(2)由1中求得回路中电流,求出安培力对M棒受力分析可得,
(3)根据能量守恒定律,求解产生的热量.
解答 解:(1)设最终速度为v,金属杆P最终匀速下滑,则有:
BIL=mgsin53°
又感应电流为:I=$\frac{E}{{R}_{1}+{R}_{2}}$
感应电动势为:E=BLv
联立解得:v=6m/s;
(2)当M棒运动到cc′时,根据对称性,对M棒受力分析,受重力和弹簧弹力F=kx=30×0.2=6N,向左的摩擦力,由左手定则判定安培力与水平方向成53°斜向右下方,由于金属杆M在cc′位置静止,则由:
BILcos53°=$\frac{{B}^{2}{L}^{2}v}{{R}_{1}+{R}_{2}}$cos53°=kxsin30°+f,
代入数据:$\frac{{1}^{2}×{2}^{2}×6}{2+1}$×0.6=30×0.2×0.5+f,
解得:f=1.8N,方向水平向左;
(3)根据能量守恒定律,可得:mgxsin53°=$\frac{1}{2}$m2v2+QP+QM+Wf;
代入数据:1×10×3×0.8=$\frac{1}{2}$×1×62+QP+QM+2
解得:QP+QM=4J
根据串并联电路特点得:QP:QM=R2:R1=2:1
联立①②解得:QP=$\frac{8}{3}$J;
答:(1)金属杆P的最终速度大小为6m/s;
(2)金属杆M在cc′位置静止时所受的摩擦力为1.8N;方向向左;
(3)金属杆P上产生的热量是$\frac{8}{3}$J.
点评 本题是力电综合题,难度适中,合理的利用法拉第电磁感应定律和牛顿第二定律及欧姆定律即可解题,关键在于分清研究对象找准规律,合理利用.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | 同时落地 | B. | 水平位移相同 | C. | 加速度不同 | D. | 着地速度相同 |
| A. | 2m/s | B. | 4m/s | C. | 6m/s | D. | 8m/s |
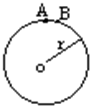 如图所示,半径为r的硬橡胶圆环,其上带有均匀分布的正电荷,单位长度的电量为q,其圆心O处的合场强为零,现截去圆环顶部的一小段AB,AB=l(l<<r),则关于剩余部分在圆心O处产生的场强,下列说法中正确的是( )
如图所示,半径为r的硬橡胶圆环,其上带有均匀分布的正电荷,单位长度的电量为q,其圆心O处的合场强为零,现截去圆环顶部的一小段AB,AB=l(l<<r),则关于剩余部分在圆心O处产生的场强,下列说法中正确的是( )| A. | O处场强方向竖直向上 | |
| B. | O处场强方向竖直向下 | |
| C. | O处场强的大小为$\frac{klq}{{r}^{2}}$(k为静电力恒量,下同) | |
| D. | O处场强的大小为kq(2πr-l)r2 |
| A. | 在电场中某点的电势为零,则该点的电场强度一定为零 | |
| B. | 电荷在电场中电势高的地方电势能大,在电势低的地方电势能小 | |
| C. | 根据公式U=Ed 知,在匀强电场中距离相等的两点,电势差一定相等 | |
| D. | 正电荷从电势高的点运动到电势低的点,电势能一定减少 |
 如图所示,一小球从斜面上的A点由静止下滑做匀变速直线运动,先后经过B、C两点,已知小球从B运动到C点的时间为t,B、C两点间的距离为s,小球到达C点时的速度为v,求小球的加速度大小.
如图所示,一小球从斜面上的A点由静止下滑做匀变速直线运动,先后经过B、C两点,已知小球从B运动到C点的时间为t,B、C两点间的距离为s,小球到达C点时的速度为v,求小球的加速度大小.






 AB两个质量均为m的小球,被一轻杆AB固定,轻杆长AB=L,OA=$\frac{L}{3}$,杆可绕O点的水平轴无摩擦地转动,初始时杆静止在竖直位置,如图所示,今在B球上施加一水平方向恒力F=$\frac{\sqrt{3}}{2}$mg,试求:
AB两个质量均为m的小球,被一轻杆AB固定,轻杆长AB=L,OA=$\frac{L}{3}$,杆可绕O点的水平轴无摩擦地转动,初始时杆静止在竖直位置,如图所示,今在B球上施加一水平方向恒力F=$\frac{\sqrt{3}}{2}$mg,试求: