Question

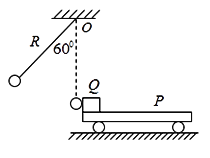
【题目】如图所示，一条不可伸长的轻绳长为R，一端悬于天花板上的O点，另一端系一质量为m的小球（可视为质点）。光滑水平面上有一质量为M的平板车 ，在其左端放有一个质量也为m的物块（可视为质点），物块处在悬点O的正下方，系统静止。现将小球拉至悬线与竖直方向成60°角时由静止释放，当小球到达最低点时刚好与物块发生弹性正碰。之后物块在平板车上运动，当它离开平板车时速度大小是平板车的两倍，物块与平板车之间的动摩擦因数为μ，M∶m=4∶1，重力加速度为g。求：

（1）小球与物块正碰后，物块的速度为多大？

（2）平板车的长度为多少？

Answer 1

【答案】（1） (2)

【解析】本题考查物体摆动、弹性碰撞以及滑块在小车上的滑行，需运用机械能守恒、动量守恒、能量转化和守恒等知识求解。

(1)设小球即将与物块碰撞前的速度为，小球由初始位置摆动到最低点的过程中，由机械能守恒定律可得： 解得：

设碰撞后小球速度为，物块速度为，由于小球与物块是弹性碰撞，所以碰撞过程满足机械能守恒和动量守恒，有： ，

联立解得： ，

即：速度交换，小球速度变为零， 获得小球的速度

（2）设离开平板车时的速度大小为，则平板车速度为，物块在小车上滑行的过程中，由动量守恒定律可得： ，又∶=4∶1

解得：

设平板车的长度为，由题意可得物块在小车上滑行时，减少的动能转化为系统的内能，所以有： ，解得： 。