题目内容
 在平直的公路上,汽车由静止开始做匀加速直线运动,当速度达到v时,关闭发动机,汽车向前滑行直到停止,其运动的v-t图线如图所示.已知汽车的牵引力大小为F,所受摩擦阻力为Ff,全过程中牵引力做功W1,克服阻力做功为W2,则( )
在平直的公路上,汽车由静止开始做匀加速直线运动,当速度达到v时,关闭发动机,汽车向前滑行直到停止,其运动的v-t图线如图所示.已知汽车的牵引力大小为F,所受摩擦阻力为Ff,全过程中牵引力做功W1,克服阻力做功为W2,则( )分析:由速度-时间图象可知物体的运动状态,找出加速与减速过程中位移之比;分析汽车的受力情况及各力的做功情况,由动能定理可得出牵引力及克服阻力做功的比值.
解答:解:由图可知,物体先做匀加速直线运动,1s末速度为v,由动能定理可知:
(F-Ff)L1=
mv2;
减速过程中,只有阻力做功:
FfL2=0-
mv2;
则可得:(F-Ff)L1=FfL2;
由图象可知,L1:L2=1:3;
解得:
=
;
对全程由动能定理得:
W1-W2=0
故
=1;
所以选项AD错误,BC正确.
故选BC.
(F-Ff)L1=
| 1 |
| 2 |
减速过程中,只有阻力做功:
FfL2=0-
| 1 |
| 2 |
则可得:(F-Ff)L1=FfL2;
由图象可知,L1:L2=1:3;
解得:
| F |
| Ff |
| 4 |
| 1 |
对全程由动能定理得:
W1-W2=0
故
| W1 |
| W2 |
所以选项AD错误,BC正确.
故选BC.
点评:动能定理应用时要注意灵活选取研究过程,一般全程应用动能定理更简单;但本题中由于要求出各力之比,故还要分段列出.对于B选项的分析还可以用动量守恒解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在平直的公路上,汽车由静止开始做匀加速运动,当速度达到Vm,立即关闭发动机而滑行直到停止,v-t 图线如图,汽车的牵引力大小为F1,摩擦力大小为F2,全过程中,牵引力做功为W1,克服摩擦力做功为W2,则( )
在平直的公路上,汽车由静止开始做匀加速运动,当速度达到Vm,立即关闭发动机而滑行直到停止,v-t 图线如图,汽车的牵引力大小为F1,摩擦力大小为F2,全过程中,牵引力做功为W1,克服摩擦力做功为W2,则( ) 在平直的公路上,汽车由静止开始做匀加速运动.当速度达到Vm后,立即关闭发动机而滑行直到停止.V-t图线如图所示,汽车的牵引力大小为F1,摩擦力大小为F2.全过程中,牵引力做的功为W1,克服摩擦阻力做功为W2.以下是F1、F2及W1、W2间关系的说法,其中正确的是( )
在平直的公路上,汽车由静止开始做匀加速运动.当速度达到Vm后,立即关闭发动机而滑行直到停止.V-t图线如图所示,汽车的牵引力大小为F1,摩擦力大小为F2.全过程中,牵引力做的功为W1,克服摩擦阻力做功为W2.以下是F1、F2及W1、W2间关系的说法,其中正确的是( )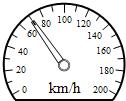 在平直的公路上,汽车启动后在第10s末,速度表的指针指在如图所示的位置,前10s内汽车运动的距离为150m.则第10s末汽车的瞬时速度是
在平直的公路上,汽车启动后在第10s末,速度表的指针指在如图所示的位置,前10s内汽车运动的距离为150m.则第10s末汽车的瞬时速度是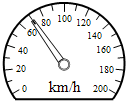 在平直的公路上,汽车启动后在第10s末,速度表的指针指在如图所示的位置,前10s内汽车运动的距离为150m.下列说法中正确的是( )
在平直的公路上,汽车启动后在第10s末,速度表的指针指在如图所示的位置,前10s内汽车运动的距离为150m.下列说法中正确的是( )