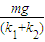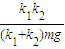题目内容
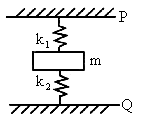
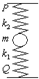 如图所示,两个弹簧的质量不计,劲度系数分别为k1、k2,它们的一端固定在质量为m的物体上,另一端分别固定在P、Q点,当物体平衡时,上面的弹簧k2处于原长,若要把物体的质量换成2m(它的厚度不变,且均在弹簧的弹性限度内),再次平衡时,物体比第一次平衡时下降的距离x为( )
如图所示,两个弹簧的质量不计,劲度系数分别为k1、k2,它们的一端固定在质量为m的物体上,另一端分别固定在P、Q点,当物体平衡时,上面的弹簧k2处于原长,若要把物体的质量换成2m(它的厚度不变,且均在弹簧的弹性限度内),再次平衡时,物体比第一次平衡时下降的距离x为( )分析:当物体的质量为m时,弹簧k2处于原长,下方弹簧的弹力等于mg,由胡克定律求出其压缩的长度.将物体的质量增为原来的2倍时,上方的弹簧伸长的长度与下方弹簧压缩量增加的长度相等,等于物体下降的高度,两弹簧弹力之和等于2mg,再由胡克定律求解物体下降的高度.
解答:解:当物体的质量为m时,下方弹簧被压缩的长度为x2=
①
当物体的质量变为2m时,设物体下降的高度为x,则上方弹簧伸长的长度为x,下方弹簧被压缩的长度为x2+x,两弹簧弹力之和等于2mg由胡克定律和平衡条件得:
k1x+k2(x2+x)=2mg ②
由①②联立解得,x=
故选A
| mg |
| k2 |
当物体的质量变为2m时,设物体下降的高度为x,则上方弹簧伸长的长度为x,下方弹簧被压缩的长度为x2+x,两弹簧弹力之和等于2mg由胡克定律和平衡条件得:
k1x+k2(x2+x)=2mg ②
由①②联立解得,x=
| mg |
| k1+k2 |
故选A
点评:本题由胡克定律和平衡条件分别研究两种情况下弹簧的压缩量,要抓住第二情况下,两弹簧形变量与物体下降高度相等进行列式.

练习册系列答案
相关题目
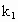 、
、 ,它们一端固定在质量为m的物体上,另一端分别固定在P、Q上,当物体平衡时上面的弹簧(
,它们一端固定在质量为m的物体上,另一端分别固定在P、Q上,当物体平衡时上面的弹簧(