题目内容
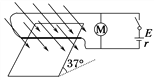
【题目】如图甲所示的陀螺可在圆轨道外侧旋转而不脱落,好像轨道对它施加了魔法一样,被称为“魔力陀螺”.它可等效为如图乙所示的模型:竖直固定的磁性圆轨道半径为R,质量为m的质点在轨道外侧做完整的圆周运动,A、B两点分别为轨道上的最高与最低点.质点受轨道的磁性引力始终指向圆心O且大小恒定,不计摩擦和空气阻力,重力加速度为g.
(1)判断质点运动过程中机械能是否守恒,并说明理由;
(2)若磁性引力的大小为10mg,质点在A点的速度为![]() ,求质点在该点对轨道的弹力;
,求质点在该点对轨道的弹力;
(3)求满足质点做完整圆周运动时磁性引力的最小值.

【答案】(1)机械能守恒 (2)10mg,方向竖直向下 (3)5mg
【解析】试题分析:因为质点运动过程中只有重力做功,所以质点的机械能守恒;在A点,由合力提供向心力,由牛顿第二定律求出轨道对质点的弹力,再由牛顿第三定律得到质点对轨道的弹力.若磁性引力大小F可变,质点仍做完整圆周运动,质点在B点不脱离轨道即可,到达B点的速度最小,机械能守恒定律与牛顿第二定律求解。
(1)为质点运动过程中只有重力做功,所以质点的机械能守恒
(2)在A点时,设轨道对质点有向上的大小为FN的弹力.
根据牛顿第二定律得: ![]()
代入数据计算得出:FN=10mg
由牛顿第三定律得,质点对轨道的弹力大小为10mg,方向竖直向下.
(3)质点在B点不脱离轨道即可,当vA=0,到达B点的速度最小,
根据机械能守恒定律得: ![]()
设磁性引力为F,在B点有: ![]()
所以有:F=5mg+ FN
当FN=0时,磁性引力最小,故得:Fmin=5mg

练习册系列答案
相关题目