题目内容
(2010?烟台一模)如图所示,在真空中,边长为2b的虚线所围的正方形区域ABCD内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距离为b,板长为2b,O1O2为两板的中心线.且O1为磁场右边界BC边的中点.有一电荷量为q、质量为m的带正电的粒子,以速度v0从DC边某点P点沿垂直于DC的方向进入磁场,当粒子从O1点沿O1O2方向飞出磁场的同时,给M、N板间加上如图所示交变电压u(图中U0与T未知).最后粒子刚好以平行于N板的速度,从N板的边缘飞出.不计平行金属板两端的边缘效应及粒子所受的重力.求:
(1)磁场的磁感应强度B的大小;
(2)交变电压的周期T和电压U0的值;
(3)若t=
时,将相同粒子从MN板右侧O2点沿板的中心线O2O1方向,仍以速率v0射入M、N之间,求粒子进入磁场后在磁场中运动的时间.

(1)磁场的磁感应强度B的大小;
(2)交变电压的周期T和电压U0的值;
(3)若t=
| T | 2 |

分析:粒子进入磁场在洛伦兹力作用下做匀速圆周运动,完成
圆弧后,垂直进入匀强电场后做类平抛运动,最后只好从N板边缘飞出,由平抛运动规律可求出运动的时间,从而得出电场变化的周期,最终列出极板间电压的表达式.
当t=
粒子以速度v0沿O2O1射入电场时,则该粒子将恰好从M板边缘以平行于极板的速度射入磁场,根据粒子运动轨道结合几何关系可求出圆周运动的周期,从而算出运动的时间.
| 1 |
| 4 |
当t=
| T |
| 2 |
解答:解:粒子自P点进入磁场,从O1点水平飞出磁场,运动半径为b,
则qv0B=m
解得:B=
粒子自O1点进入电场,最后恰好从N板的边缘平行飞出,
设运动时间为t,则2b=v0t
=2n?
?
(
)2
t=nT(n=1,2,…)
解得:T=
(n=1,2,…)
U0=
(n=1,2,…)
(3)当t=
粒子以速度v0沿O2O1射入电场时,则该粒子将恰好从M板边缘以平行于极板的速度射入磁场,且进入磁场的为v0,运动的轨道半径仍为b,设进入磁场的点为E,离开磁场的点为Q,圆心为O,
如图所示,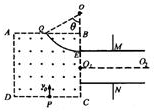
OB=R-
=
OQ=R=b
由cosθ=
=
可得:θ=60°=
因为T=
,
得T=
粒子在磁场中运动的时间为t=
T=
=
.
则qv0B=m
| ||
| b |
解得:B=
| mv0 |
| bq |
粒子自O1点进入电场,最后恰好从N板的边缘平行飞出,
设运动时间为t,则2b=v0t
| b |
| 2 |
| 1 |
| 2 |
| qU0 |
| mb |
| T |
| 2 |
t=nT(n=1,2,…)
解得:T=
| 2b |
| nv0 |
U0=
nm
| ||
| 2q |
(3)当t=
| T |
| 2 |
如图所示,

OB=R-
| b |
| 2 |
| b |
| 2 |
由cosθ=
| OB |
| OQ |
| 1 |
| 2 |
可得:θ=60°=
| π |
| 3 |
因为T=
| 2πR |
| v0 |
得T=
| 2πb |
| v0 |
粒子在磁场中运动的时间为t=
| θ |
| 2π |
| T |
| 6 |
| πb |
| 3v0 |
点评:本题突破口:粒子自O1点进入电场,最后恰好从N板的边缘平行飞出;当t=
粒子以速度v0沿O2O1射入电场时,则该粒子将恰好从M板边缘以平行于极板的速度射入磁场.
| T |
| 2 |

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
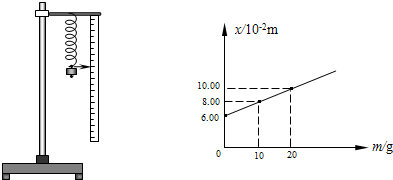
 (2010?烟台一模)小木块放在倾角为α的斜面上,受到一个水平力F ( F≠0 )的作用而处于静止状态,如图所示.若小木块受到的支持力与摩擦力的合力为F合,则F合的方向及其与竖直向上方向的夹角β可能是( )
(2010?烟台一模)小木块放在倾角为α的斜面上,受到一个水平力F ( F≠0 )的作用而处于静止状态,如图所示.若小木块受到的支持力与摩擦力的合力为F合,则F合的方向及其与竖直向上方向的夹角β可能是( ) (2010?烟台一模)在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为
(2010?烟台一模)在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为