题目内容
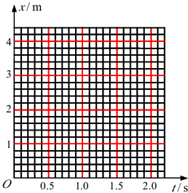一个质量为0.4kg的小球B静止在光滑的水平面上，另一个质量为0.2kg 的小球A，以3.0m/s的水平速度从C处出发做匀速直线运动，经过ls与B相撞，碰撞后A以 1.0m/s的速度反向弹回．请在坐标系上作出A、B的位置x与时间t的关系图象（以C处位置坐标为零，A球初始运动方向为x正方向）．分析：碰撞过程中动量守恒，由动量守恒定律可以求出小球B速度．
根据物体的运动性质作出位置x与时间t的关系图象．
根据物体的运动性质作出位置x与时间t的关系图象．
解答：解：碰撞过程，A球初始运动方向为x正方向，
由动量守恒定律得：mAvA=mAvA′+mBvB，
代入数据解得：vB=2m/s
所以碰撞后A以 1.0m/s的速度反向弹回．B以2m/s的速度向前运动．
A、B的位置x与时间t的关系图象：
答：在坐标系上作出A、B的位置x与时间t的关系图象如上图．
由动量守恒定律得：mAvA=mAvA′+mBvB，
代入数据解得：vB=2m/s
所以碰撞后A以 1.0m/s的速度反向弹回．B以2m/s的速度向前运动．
A、B的位置x与时间t的关系图象：
答：在坐标系上作出A、B的位置x与时间t的关系图象如上图．
点评：小球碰撞过程中动量守恒，由动量守恒定律可以正确解题，应用动量守恒定律解题时要注意正方向的选择．
练习册系列答案
名校课堂系列答案
相关题目
（选修模块3-5）
如图所示，与水平面成37°的倾斜轨道AB，其延长线在C点与半圆轨道CD（轨道半径R=1m）相切，全部轨道为绝缘材料制成且放在竖直面内．整个空间存在水平向左的匀强电场，MN的右侧存在垂直纸面向里的匀强磁场．一个质量为0.4kg的带电小球沿斜面下滑，至B点时速度为VB=100/7 m/s，接着沿直线BC（此处无轨道）运动到达C处进入半圆轨道，进入时无动能损失，且刚好到达D点，从D点飞出时磁场消失，不计空气阻力，取g=10m/s2，cos37°=0.8，求：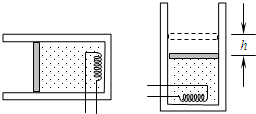
[选做题]本题包括A、B、C三小题，请选定其中两题，并在相应的答题区域内作答．若三题都做，则按A、B两题评分．
