题目内容
13.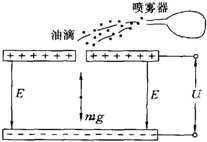 美国物理学家密立根早在1911年以著名的油滴实验,推断自然界存在基本电荷,并测得了基本电荷的电荷量,其实验过程如下:水平放置的两平行绝缘金属板间距为d,在上极板的中间开一小孔,使质量为m的微小带电油滴从这个小孔落到极板中,忽略空气浮力,当极板上没加电压时,由于空气阻力大小与速度大小成正比(设比例系数为k,且k>0),经过一段时间后即可观察到油滴以恒定的速度υ1在空气中缓慢降落.
美国物理学家密立根早在1911年以著名的油滴实验,推断自然界存在基本电荷,并测得了基本电荷的电荷量,其实验过程如下:水平放置的两平行绝缘金属板间距为d,在上极板的中间开一小孔,使质量为m的微小带电油滴从这个小孔落到极板中,忽略空气浮力,当极板上没加电压时,由于空气阻力大小与速度大小成正比(设比例系数为k,且k>0),经过一段时间后即可观察到油滴以恒定的速度υ1在空气中缓慢降落.①极板上加电压U时可见到油滴以恒定的速率υ2缓慢上升,试求油滴所带电荷量q(用d,U,k,υ1,υ2等已知量表示)
②在极板上不加电压时,油滴在极板内以恒定的速率υ1下降时,移动某一定值的竖直距离所需时间为t1,加了电压U后以恒定速率υ2上升同一竖直距离所需时间为t2,然后又把电压撤除,使所考察的油滴又降落,并在极板内照射X射线以改变它的带电荷量,再在极板上加上同样的电压U,重复上述操作,测定油滴上升及下降的时间,即可发现($\frac{1}{t_1}+\frac{1}{t_2}$)始终是0.005 35s-1的整数倍,由此可断定:一定存在基本电荷(最小单元电荷),若已知d=2×10-2 m,m=3.2×10-16kg,t1=11.9s,U=25V,取g=9.8m/s2,试计算基本电荷的带电荷量?
分析 (1)当极板上没加电压时,油滴以恒定的速率v在空气中缓慢降落,重力与空气阻力平衡,根据平衡条件求出重力.当极板上加电压u时,油滴以恒定的速率v2缓慢上升,电场力与重力和空气阻力的合力平衡,再由平衡条件求解电量.
(2)根据油滴通过某一定值的竖直距离时,以恒定的速率v1下降时所需时间为t1,恒定速率v2上升同一竖直距离所需时间为t2,根据两个时间的关系式.再由($\frac{1}{{t}_{1}}$+$\frac{1}{{t}_{2}}$)始终是0.00535s-1的整数倍,得出电量的表达式,求解基元电荷的带电量
解答 解:
(1)当极板上没加电压时,得到:mg=kv1 ①
当极板上加电压u时,由题得;q$\frac{u}{d}$=mg+kv2 ②
由①、②得,q=$\frac{gk({v}_{1}+{v}_{2})}{u}$ ③
(2)由题意得,v1t1=v2t2 ④
($\frac{1}{{t}_{1}}$+$\frac{1}{{t}_{2}}$)=0.00535ns-1(n为整数) ⑤
由以上①-⑤式得,q=$\frac{0.00535dmg{t}_{1}n}{u}$
可见,粒子所带电量是基元电荷所带电量的整数倍,基元电荷的带电量为
e=$\frac{0.00535dmg{t}_{1}}{u}$
代入解得,e=1.6×10-19C
答:
(1)滴所带电量q=$\frac{gk({v}_{1}+{v}_{2})}{u}$.
(2)基元电荷的带电量为e=1.6×10-19C.
点评 本题题目比较长,文字较多,首先要耐心读题,其次要抓住有效信息,要具有构建物理模型的能力.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
18.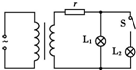 用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题.如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为r,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法正确的是( )
用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题.如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为r,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法正确的是( )
 用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题.如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为r,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法正确的是( )
用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题.如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为r,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法正确的是( )| A. | 原线圈中电流减小 | B. | r两端的电压增大 | ||
| C. | 原线圈输入功率不变 | D. | 副线圈输出电压减小 |
5.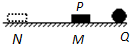 如图,在粗糙绝缘水平面上固定一点电荷Q,在M点无初速度地释放带电小物块P,P将沿水平面运动到N点静止,则从M到N的过程中( )
如图,在粗糙绝缘水平面上固定一点电荷Q,在M点无初速度地释放带电小物块P,P将沿水平面运动到N点静止,则从M到N的过程中( )
 如图,在粗糙绝缘水平面上固定一点电荷Q,在M点无初速度地释放带电小物块P,P将沿水平面运动到N点静止,则从M到N的过程中( )
如图,在粗糙绝缘水平面上固定一点电荷Q,在M点无初速度地释放带电小物块P,P将沿水平面运动到N点静止,则从M到N的过程中( )| A. | P所受库仑力逐渐减小 | |
| B. | P的电势能一定增加 | |
| C. | M、N 两点的电势φM一定高于φN | |
| D. | 克服摩擦力做的功等于电势能的减少 |
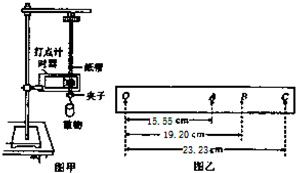 用如图甲所示的实验装置验证机械能守恒定律,质量m=100g的重物拖动纸带自由下落,打点计时器在纸带上打出一系列点.如图乙所示为选取的一条符合实验要求的纸带,O 点为打出的第一个点,A、B、C为从合适位置开始选取的三个连续的点(其它点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/s2.那么:
用如图甲所示的实验装置验证机械能守恒定律,质量m=100g的重物拖动纸带自由下落,打点计时器在纸带上打出一系列点.如图乙所示为选取的一条符合实验要求的纸带,O 点为打出的第一个点,A、B、C为从合适位置开始选取的三个连续的点(其它点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/s2.那么: 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,则小球的加速度为0.5m/s2,小球经b点时的速度为$\sqrt{10}$m/s,小球经c点时的速度为3m/s.
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,则小球的加速度为0.5m/s2,小球经b点时的速度为$\sqrt{10}$m/s,小球经c点时的速度为3m/s. 某同学为了测量一个额定率为1W的电阻Rx的阻值,先多用表的欧姆档进行了粗测,然后用伏安法进行精确测量.
某同学为了测量一个额定率为1W的电阻Rx的阻值,先多用表的欧姆档进行了粗测,然后用伏安法进行精确测量.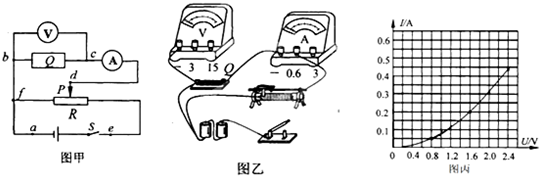
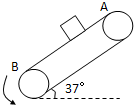 如图所示,传送带与地面成夹角θ=37°,从A到B长度为8.8m,传送带以6m/s的速率逆时针转动.在传送带上端A无初速度地放一个质量为0.4kg的黑色煤块,它与传送带之间的动摩擦因数为0.5,sin37°=0.6,cos37°=0.8,g=10m/s2,试求:
如图所示,传送带与地面成夹角θ=37°,从A到B长度为8.8m,传送带以6m/s的速率逆时针转动.在传送带上端A无初速度地放一个质量为0.4kg的黑色煤块,它与传送带之间的动摩擦因数为0.5,sin37°=0.6,cos37°=0.8,g=10m/s2,试求: