题目内容

(1)试求小球释放过程中电势能的最大变化量?
(2)若小球刚到最低点时,被一颗水平飞来的子弹击中(子弹未穿出),碰撞时间极短;设子弹的初速度v0=
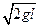 、质量为m、电量为q=Q/2。试求:
、质量为m、电量为q=Q/2。试求:①悬线偏离竖直线多大的角度时,小球有最大的速度?
②小球对悬线的最大拉力为多大?
(1)mgl(2)①θ=370②4.5mg
(1)设球静止时的位置悬线与竖直线成α角,因E=mg/Q,
则: (1分)
(1分)
那么小球从静止释放后,将恰能运动到最低点,此过程中电场力做功:
W=-EQl (1分)
故小球释放过程中电势能的最大变化量将增加△EP=-W= EQl="mgl " (2分)
(2)当小球与子弹相碰后,整体的质量m总=2m,电荷量Q总=3Q/2 (2分)
①由振动知识可知:小球速度最大的位置在振动的平衡,那么设球静止时的位置悬线与竖直线成θ角,则有: (1分)
(1分)
θ=370 (1分)
②设悬线对小球的最大拉力为T,由圆周运动知识可知:小球速度最大的位置即为悬线所受最大拉力的位置,
碰撞过程中:由动量守恒有mv0 =2 mv共 (1分)
上摆过程中:由动能定理有EQ总lsinθ-m总gl (1-cosθ)= m总v2-
m总v2- m总v
m总v
(1分)
小球在平衡位置时:T-EQ总sinθ-m总gcosθ=m总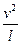 (1分)
(1分)
解得:T=4.5mg (1分)
由牛三定律:小球对悬线的最大拉力为4.5mg (1分)
则:
 (1分)
(1分)那么小球从静止释放后,将恰能运动到最低点,此过程中电场力做功:
W=-EQl (1分)
故小球释放过程中电势能的最大变化量将增加△EP=-W= EQl="mgl " (2分)
(2)当小球与子弹相碰后,整体的质量m总=2m,电荷量Q总=3Q/2 (2分)
①由振动知识可知:小球速度最大的位置在振动的平衡,那么设球静止时的位置悬线与竖直线成θ角,则有:
 (1分)
(1分)θ=370 (1分)
②设悬线对小球的最大拉力为T,由圆周运动知识可知:小球速度最大的位置即为悬线所受最大拉力的位置,
碰撞过程中:由动量守恒有mv0 =2 mv共 (1分)
上摆过程中:由动能定理有EQ总lsinθ-m总gl (1-cosθ)=
 m总v2-
m总v2- m总v
m总v
(1分)
小球在平衡位置时:T-EQ总sinθ-m总gcosθ=m总
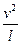 (1分)
(1分)解得:T=4.5mg (1分)
由牛三定律:小球对悬线的最大拉力为4.5mg (1分)

练习册系列答案
相关题目
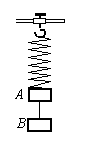
 圆弧ab,ab粗糙,ab的半径为R=0.1m。一质量为m=2.0kg的小滑块B(大小不计)以初速度
圆弧ab,ab粗糙,ab的半径为R=0.1m。一质量为m=2.0kg的小滑块B(大小不计)以初速度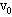 =4m/s水平向右冲上A的ab并在ab上滑动,当B离开b端后升至最大高度离b端的高度为h=0.05m。求B在A的ab上滑动过程中:
=4m/s水平向右冲上A的ab并在ab上滑动,当B离开b端后升至最大高度离b端的高度为h=0.05m。求B在A的ab上滑动过程中: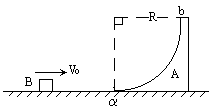
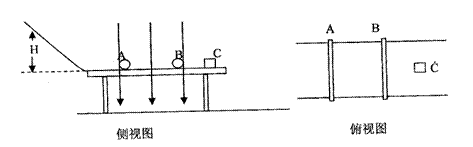

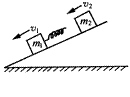
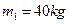 ,在滑板右端A壁左侧有一质量为
,在滑板右端A壁左侧有一质量为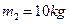 ,带电荷量为q=+2C的小铁块,在小铁块与A壁之间夹有一小堆火药,整个装置始终处于场强为E=10N/C的水平向右的匀强电场中。初始时刻,使滑板与小铁块都处于静止,现点燃火药。设火药爆炸时有100J的能量转化为滑板和小铁块的机械能,滑板水平部分足够长,小铁块和火药的体积大小、小铁块与滑板面的摩擦均不计,火药爆炸的作用力远大于电场力,爆炸后,滑板和小铁块质量、形状均不变,小铁块没有电量损失,小铁块始终未脱离滑板。
,带电荷量为q=+2C的小铁块,在小铁块与A壁之间夹有一小堆火药,整个装置始终处于场强为E=10N/C的水平向右的匀强电场中。初始时刻,使滑板与小铁块都处于静止,现点燃火药。设火药爆炸时有100J的能量转化为滑板和小铁块的机械能,滑板水平部分足够长,小铁块和火药的体积大小、小铁块与滑板面的摩擦均不计,火药爆炸的作用力远大于电场力,爆炸后,滑板和小铁块质量、形状均不变,小铁块没有电量损失,小铁块始终未脱离滑板。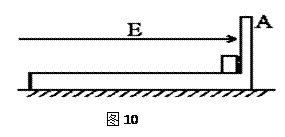

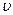 ,导体棒ab的动能为EK,此过程中两根导体棒、导体棒与磁铁之间没有发生碰撞,求
,导体棒ab的动能为EK,此过程中两根导体棒、导体棒与磁铁之间没有发生碰撞,求