题目内容
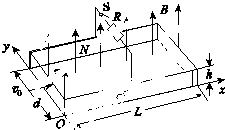
【题目】如图所示,两根平行导轨固定在倾角θ=30°的斜面上,间距d=0.4m.导轨由两部分组成,虚线MN为两部分的分界线.MN以下导轨由金属材料制成,其长度L=1.0m,电阻不计,底端接有一只标称值为“2V 0.5A”的小灯泡;MN以上导轨足够长,由绝缘材料制成.整个空间存在垂直斜面向上的匀强磁场.现将质量m=0.1kg、电阻不计的光滑导体棒从绝缘导轨上某位置由静止释放,当ab通过MN后小灯泡立即正常发光且亮度保持不变,直至ab离开轨道.ab在滑动过程中始终与导轨垂直且两端与导轨保持良好接触,取g=10m/s2 , 试求: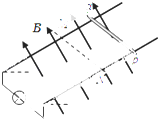
(1)ab从绝缘导轨上释放时的位置与MN相距多远?
(2)若有与ab相同的光滑导体棒若干,每隔多长时间释放一根才能使小灯泡持续正常发光?该发电装置的效率多大?
【答案】
(1)解:由题意知ab滑过MN之后做匀速直线运动,根据平衡条件有
F安=mgsinθ
导体棒所受的安培力 F安=BIL
ab棒的感应电动势 E=BLv
设ab从绝缘导轨上释放时的位置与MN相距x,由机械能守恒定律得
mgxsinθ= ![]()
联立解得 v=2m/s,x=0.4m
答:ab从绝缘导轨上释放时的位置与MN相距0.4m.
(2)解:按题意,前一根导体棒刚离开导轨后一根刚通过分界线MN,故时间相隔
△t= ![]() =0.5s
=0.5s
该发电装置的效率为
η= ![]() =71.4%
=71.4%
答:若有与ab相同的光滑导体棒若干,每隔0.5s时间释放一根才能使小灯泡持续正常发光,该发电装置的效率为71.4%.
【解析】(1)据题意,ab通过MN后小灯泡立即正常发光且亮度保持不变,说明ab滑过MN后做匀速直线运动,根据平衡条件求出ab的速度,再对ab在MN上部运动的过程,由机械能守恒求解.(2)要使小灯泡持续正常发光,前一根导体棒刚离开导轨后一根刚通过分界线MN,由匀速直线运动的规律求时间,根据有用功与总功之比求效率.
【考点精析】通过灵活运用安培力和电磁感应与力学,掌握安培力做功与路径有关,绕闭合回路一周,安培力做的功可以为正,可以为负,也可以为零,而不像重力和电场力那样做功总为零;用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向;求回路中电流强度;分析研究导体受力情况(包含安培力,用左手定则确定其方向);列动力学方程或平衡方程求解即可以解答此题.