题目内容
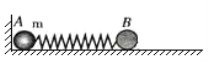
【题目】如图所示,竖直墙面和水平地面均光滑,质量分别为mA=m,mB=2m的A、B两小球如图所示放置,其中A紧靠墙壁,AB之间有质量不计的轻弹簧相连。对B物体施加一个水平向左的推力,使AB之间弹簧被压缩但系统静止,此时弹簧的弹性势能为EP,后突然撤去向左推力解除压缩,求:
(1)从撤去外力到物块A运动,墙壁对A的冲量大小?
(2)AB都运动后,B小球的最小速度是多少?
【答案】(1)2![]() (2)
(2) ![]()
![]()
【解析】
撤去推力后,B在弹力的作用下做加速运动.此过程中墙给A的冲量即为系统动量的变化,根据动量定理求解;A离开墙后,在弹簧的作用下速度逐渐增大,B的速度逐渐减小,当弹簧再次恢复原长时,A达到最大速度,B速度减小到最小值,根据系统动量守恒、机械能守恒求解。
(1) 撤去外力后,物体B在弹力作用下做加速运动。在弹簧恢复原长的过程中,系统的机械能守恒。设弹簧恢复原长时,物体B的速度为![]() 有:EP=
有:EP=![]() .2m
.2m![]()
解得:vB0=![]()
此过程中墙对A的冲量大小等于弹簧对A的冲量大小,也等于弹簧对B的冲量大小,则
I=2mvB0=2![]()
(2) 物体A离开墙壁后,弹簧伸长,A的速度逐渐增大,B的速度逐渐减小。当弹簧恢复原长时,物体A达到最大速度vA,物体B的速度减小到最小值vB , 在此过程中系统的动量守恒有:2mvB0=mvA+2mvB![]()
机械能守恒有:![]() .2m
.2m![]() =
=![]() m
m![]() +
+![]() .2m
.2m![]()
联立解得:vB=![]()
![]()
所以B的最小速度为![]()
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目