Question

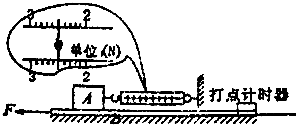
在一次课外活动中，某同学用图甲所示装置测量放在水平光滑桌面上铁块A与金属板B间的动摩擦因数．已知铁块A的质量m_A=1.0kg，金属板B的质量m_B=0.50kg．用水平力F向左拉金属板B，使其向左运动，弹簧秤的示数如图甲所示，则A、B间的摩擦力f=

3.00

N，A、B间的动摩擦因数μ=

0.30

．（g取10m/s²）．该同学还将纸带连接在金属板B的后面，通过打点计时器连续打下一系列的点，测量结果如图乙所示，图中各计数点间的时间间隔为0.10s，可求得金属板B运动的加速度a=

2.0

m/s²，拉金属板的水平拉力F=

4.0

N．

Answer 1

分析：（1）拉动B过程中，A处于平衡状态，其所受滑动摩擦力大小等于弹簧秤示数，据此可正确解答．
（2）根据△x=aT²求出金属板的加速度，然后根据牛顿第二定律，即可求出水平拉力大小．

解答：解：（1）A处于平衡状态，所受摩擦力等于弹簧秤示数，F_f=F=3.00N．
根据F_f=m_Agμ，
解得：μ=0.30．
（2）由题意可知，金属板做匀加速直线运动，根据△x=aT²，
其中△x=2cm=0.02m，T=0.1s，
所以解得：a=2.0m/s²．
根据牛顿第二定律得：F-F_f=m_Ba，
带入数据解得F=4.0N．
故答案为：3.00；     0.30；    2.0；    4.0；

点评：本题借助实验考查了基本规律的应用，平时训练中一定要加强应用基本规律解决实际问题的能了，强调知识的活学活用．