题目内容
（2011?南县模拟）2010年10月13日，智利矿难中受困69天的33名矿工陆续乘坐智利军方的“凤凰号”救生舱，由625m深的地底升井获救，创造了世界矿难救援的奇迹，若救生舱在升井过程中的最大速度为5m/s，加速和减速过程的最大加速度均为1m/s2，则救生舱将一名矿工自井底升至井口停下所需的时间至少约为（ ）
分析：该题救生舱先做匀加速，后做匀速，再做匀减速运动，具有对称性．
解答：解：匀加速上升和匀减速上升时间均为 t1=
=
s=5s
匀加速上升和匀减速上升位移均为 s′=
at2=12.5m
所以匀速用时 t2=
=120s
则自井底升至井口停下所需的时间至少约为 t=t2+2t1=130s
故选A．
| v |
| a |
| 5 |
| 1 |
匀加速上升和匀减速上升位移均为 s′=
| 1 |
| 2 |
所以匀速用时 t2=
| s-2s′ |
| v |
则自井底升至井口停下所需的时间至少约为 t=t2+2t1=130s
故选A．
点评：此题既可用运动学公式来求，也可用图象法来求．
练习册系列答案
相关题目
（2011?南县模拟）如图是法拉第研制成的世界上第一台发电机模型的原理图．将铜盘放在磁场中，让磁感线垂直穿过铜盘，图中a、b导线与铜盘的中轴线处在同一平面内，转动铜盘，就可以使闭合电路获得电流．若图中铜盘半径为L，匀强磁场的磁感应强度为B，回路总电阻为R，从上往下看逆时针匀速转动铜盘的角速度为ω．则下列说法正确的是（ ）
（2011?南县模拟）在粗糙的斜面上固定一点电荷 Q．在 M 点无初速度的释放带有恒定电荷的小物块，小物块在 Q 的电场中沿斜面运动到 N 点静止．则从 M 到 N 的过程中（ ）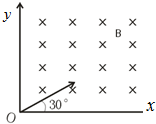
（2011?南县模拟）如图所示，在第一象限内有垂直纸面向里的匀强磁场，一对正、负电子分别以相同速度沿与x轴成30°角从原点垂直射入磁场，则正、负电子在磁场中运动时间之比为（ ）
（2011?南县模拟）一质量m=0.5kg的滑块以一定的初速度冲上一倾角为30°足够长的斜面，某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度，如图所示为通过计算机绘制出的滑块上滑过程的v-t图．求：（g取10m/s2）