��Ŀ����
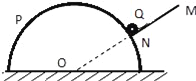
����Ŀ����ͼ��ʾ��ˮƽ��Ե���AB�봦����ֱƽ���ڵİ�Բ�ξ�Ե�⻬���BCƽ������,��Բ�ι���İ뾶R��0.4m��������ڿռ����ˮƽ���ҵ���ǿ�糡���糡ǿ��E��1.0��104 N/C������һ�����q��1.0��10��4 C������m��0.1kg�Ĵ�����(����Ϊ�ʵ�),��ˮƽ����ϵ�P���ɾ�ֹ�ͷ����������˶���Բ�ι����͵�Bʱ���ٶ���B��5 m/s����֪��������ˮƽ�����Ķ�Ħ������Ϊ0.5���������ٶ�g��10 m/s2����:

(1)�������˶���Բ�ι������͵�Bʱ��Բ�ι���Դ�����֧�����Ĵ�С;
(2)��������ˮƽ����ϵ��ͷŵ�P��B��ľ���;
(3)�������һ�ξ���C���������ˮƽ����ϵ�λ�õ�B��ľ�����
���𰸡���1��6N����2��2m����3��![]()
��������
���⣨1���������ͨ��C��ʱ���ٶ�Ϊ![]() ������ţ�ٵڶ�����
������ţ�ٵڶ�����
![]() ��1�֣�
��1�֣�
�������ͨ��B��ʱ���ٶ�Ϊ![]() �������Դ������֧������СΪ
�������Դ������֧������СΪ![]() ���������B��ʱ��
���������B��ʱ��
����ţ�ٵڶ�����![]() ��1�֣�
��1�֣�
�������B�˶���C�����У����ݶ��ܶ�����![]() ��2�֣�
��2�֣�
�������![]() =6N ��1�֣�
=6N ��1�֣�
��2����PB��ľ���ΪS ,��![]() ��2�֣�
��2�֣�
��ã�s=2m ��1�֣�
��3������������ߵ�C����ˮƽ����ϵ�d�㾭��ʱ��Ϊt�������˶��ķֽ��У�
��ֱ����![]() ��1�֣�
��1�֣�
ˮƽ����![]() ��2�֣�
��2�֣�
������![]() ��1�֣�
��1�֣�

 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�