题目内容
A，B两个滑块在粗糙的水平面上一前一后减速向右滑行，向右建立x坐标，两个滑块在运动过程中的坐标随时间关系为xA=10+4t-2t2(m)，xB=16t-4t2(m)，则可以判断它们能相遇几次（ ）
分析：当两个滑块满足条件xA=xB时，两者相遇，求出时间可能的值．再分析在这个时间内两个滑块是否停止运动，选择实际的时间值，判断相遇几次．
解答：解：当xA=xB时，两滑块相遇，即有10+4t+t2=16t-4t2，解得t1=6s，t2=1s
由两坐标的表达式得到：
A的初速度为vA=4m/s，加速度为aA=-4m/s2，则A滑行时间为tA=
=1s
B的初速度为vB=16m/s，加速度为aB=-4m/s2，则B滑行时间为tB=
=4s，则4s后B停止运动，所以t1=6s不合理，舍去，由于相遇的时间只有一个值，说明两滑块只能相遇一次．
故选B
由两坐标的表达式得到：
A的初速度为vA=4m/s，加速度为aA=-4m/s2，则A滑行时间为tA=
| 0-vA |
| aA |
B的初速度为vB=16m/s，加速度为aB=-4m/s2，则B滑行时间为tB=
| 0-vB |
| aB |
故选B
点评：本题是相遇问题，一方面要抓住相遇的条件：xA=xB，另一方面要注意检验解题是否合理，这是匀减速运动正常要考虑的问题．
练习册系列答案
相关题目
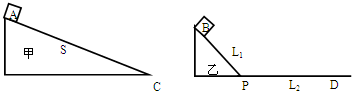
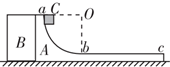如图所示，A、B两个滑块放在光滑的水平面上，将B固定不动，滑块A和B靠在一起，A上表面的ab段是半径为0.8m的四分之一光滑圆弧，bc段是粗糙的水平面，ab段与bc段相切于b点．将小滑块C从a点由静止开始下滑，已知bc段长度为2m，A和C的质量都是1kg．（取g=10m/s2）
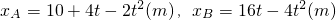，则可以判断它们能相遇几次
，则可以判断它们能相遇几次（ ）