题目内容
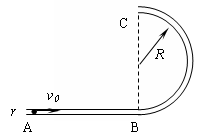
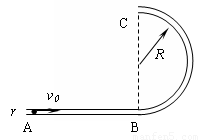
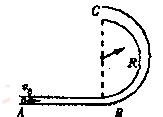
如图所示，光滑圆管形轨道AB部分平直，BC部分是处于竖直平面内半径为R的半圆，圆管截面半径r
R．有一质量为m、半径比r略小的光滑小球以水平初速v0射入圆管．
(1)若要小球能从C端出来，初速v0多大？
(2)在小球从C端出来的瞬间，对管壁压力有哪几种典型情况，初速v0各应满足什么条件？
答案：
解析：
解析：
|
小球在管内运动过程中，只有重力做功，机械能守恒，要求小球能从C端射出，小球运动到C点的速度vC＞0．根据机械能守恒定律即可算出初速v0．小球从C端射出时可能有三种典型情况：①刚好对管壁无压力；②对下管壁有压力；③对上管壁有压力．同理由机械能守恒可确定需满足的条件． 机械能守恒定律和圆周运动经常结合在一起来考查相关的题目，要注意圆周运动的特点，要分清绳和杆的区别，单侧轨道和双侧轨道的区别．还要注意的就是如果是绳子作用在物体上，物体又在竖直平面内运动，还要考虑的就是到达最高点有一个最小速度的问题，即v≥ (1)小球从A端射入后，如果刚好能到达管顶，则vC＝0，由机械能守恒，根据 可得：v0＞ 因此，要求小球能从C端出来，必须使vC＞0，所以入射速度应满足条件v0＞ (2)小球从C端出来的瞬间，可以有三种典型情况： ①刚好对管壁无压力，此时需满足条件 mg＝ 联立得入射速度v0＝ ②对下管壁有压力，此时相应的入射速度为 ③对上管壁有压力，相应的入射速度为v0＞ |
．
mv02＝mg·2R
；
练习册系列答案
相关题目
如图所示，光滑圆管形轨道AB部分平直，BC部分是处于竖直平面内半径为R的半圆，圆管截面半径r＜＜R．有一质量为m、半径比r略小的光滑小球以水平初速度v0射入圆管，问：
（1）如图所示，某种变速自行车有三个链轮和六个飞轮，链轮和飞轮的齿数如下表所示．该自行车的前后轮周长为2m，人脚踩踏板的转速为每秒钟1.5转．若采用的链轮和飞轮齿数分别为48和24，则该种组合下自行车行驶时的速度为
