题目内容
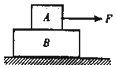
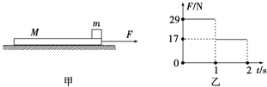
【题目】有一项“快乐向前冲”的游戏可简化如下:如图,滑板长L=1 m,起点A到终点线B的距离s=5 m。开始滑板静止,右端与A平齐,滑板左端放一可视为质点的滑块,对滑块施一水平恒力F使滑板前进。板右端到达B处冲线,游戏结束。已知滑块与滑板间动摩擦因数μ=0.5,地面视为光滑,滑块质量m1=2 kg,滑板质量m2=1 kg,重力加速度g=10 m/s2,求:
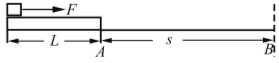
(1)滑板由A滑到B的最短时间可达多少?
(2)为使滑板能以最短时间到达,水平恒力F的取值范围如何?
【答案】(1)t=1 s (2)![]()
【解析】(1)滑板一直加速,所用时间最短。设滑板加速度为a2
f=m1g=m2a2,a2=10 m/s2
![]()
t=1 s;
(2)刚好相对滑动时,F最小,此时可认为二者加速度相等
F1–m1g=m1a2
F1=30 N
当滑板运动到B点,滑块刚好脱离时,F最大,设滑块加速度为a1
F2–m1g=m1a1
滑块运动放热位移s1=L+s=6 m,且![]() ,解得
,解得![]()
故F2=34 N。
故![]()

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
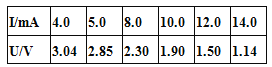
【题目】在做“探究加速度和力、质量的关系”的实验中,保持小车和砝码的总质量不变,测得小车的加速度a和拉力F的数据如下表所示
F (N) | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
a (m/s2) | 0.11 | 0.19 | 0.29 | 0.40 | 0.51 |
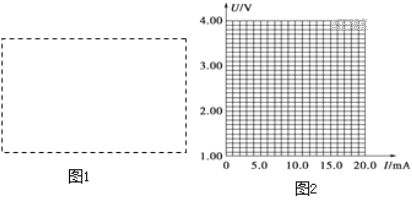
(1)根据中的数据在坐标图上作出a﹣F图象;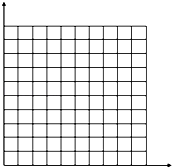
(2)图象斜率的物理意义是;
(3)小车和砝码的总质量为kg;
(4)图线(或延长线)与F轴截距的物理意义是 .