题目内容
（12分）如图所示，倾角θ=30°的光滑斜面的下端与水平地面平滑连接（可认为物体在连接处速率不变）。一个质量为m的小物体（可视为质点），从距地面h=3.2m高处由静止沿斜面下滑。物体与水平地面间的动摩擦因数为μ=0.4，重力加速度g=10m/s2，求：
（1）物体沿斜面下滑的加速度a的大小；
（2）物体下滑到达斜面底端A时速度vA的大小；
（3）物体在水平地面上滑行的时间t。
（1）a=5m/s2（2）vA=" 8m/s" （3）t=2s
解析试题分析：（1）物体由静止沿斜面下滑过程，由牛顿运动定律有：
沿斜面方向：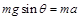
………………①
代入数据解①得：a=5m/s2 ………………②
（2）设物体由静止沿斜面下滑经时间t1至底端A处，由运动学规律有：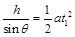
………………③
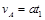………………④
联解③④式并代入数据得：vA= 8m/s ………………⑤
（3）物体在地面作匀减速运动，设加速度大小为a′，由牛顿运动定律有：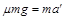
………………⑥
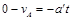………………⑦
联解⑥⑦式并代入数据得：t=2s ………………⑧
评分参考意见：本题满分12分，其中①③④⑥式各2分，②⑤⑦⑧式各1分；若有其他合理解法且答案正确，可同样给分。
考点：牛顿第二定律，运动学公式
练习册系列答案
相关题目
倍。已知杆向上运动时，刚穿过PQ时的速度是刚穿过MN时速度的一半，杆从PQ上升的最大高度（未超过轨道上端）是磁场高度的n倍；杆向下运动时，一进入磁场立即做匀速直线运动。除定值电阻外不计其它一切电阻，已知重力加速度为g。求：
