Question

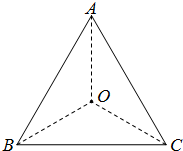如图所示，一粒子源位于一边长为a的正三角形ABC的中心O处，可以在三角形所在的平面内向各个方向发射出速度大小为v、质量为m、电荷量为q的带电粒子，整个三角形位于垂直于△ABC的匀强磁场中，若使任意方向射出的带电粒子均不能射出三角形区域，则磁感应强度的最小值为（　　）

• A、

  mv

  qa

• B、

  4 3 mv

  qa

• C、

  2 3 mv

  qa

• D、

  3 3 mv

  qa

Answer 1

分析：带电粒子垂直射入磁场中，在洛伦兹力作用下做匀速圆周运动，由r=

mv

qB

知，粒子的半径与B成反比，当粒子的轨迹恰好与△ABC的边AB相切时，其不能射出三角形区域的运动半径最大，所对应的磁感应强度的最小，由几何知识可求出半径的最大值，由牛顿第二定律可求出B的最小值．

解答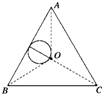：解：如图所示，带电粒子不能射出三角形区域的最大半径是r=

1

2

?

a

2

?tan30°=

3 a

12

，
由qvB=m

v2

r

得，
最小的磁感应强度是B=

4 3 mv

qa

．
故选：B．

点评：本题属于临界问题，当粒子的轨迹与边界A相切时，半径最大．本题的解题关键是作出轨迹的示意图，根据几何知识求出运动半径最大值．