题目内容
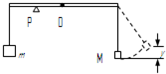（2009?上海二模）如图所示，轻杆可绕其中点O自由转动，初始时质量M=4kg的小物体通过长为R=1m的细绳挂在杆的右端，质量m=5kg的小物体通过细绳挂在杆的左端，为使轻杆水平静止，在P处将其托住．若用水平拉力缓慢拉起M，则P处受到的压力不变
不变
（填“变大”、“变小”或“不变”）；若将M拉高y后静止释放，为使杆不离开P，则y至多为0.125
0.125
m．分析：用水平拉力缓慢拉起M，由平衡条件分析细绳的拉力与小物体重力Mg的关系，再以O点为支点，根据力矩平衡条件列式，分析P对轻杆的支持力如何变化，即可得到P处所受的压力如何变化；若将M拉高y后静止释放，当杆刚离开P时，P对轻杆的支持力为零，由力矩平衡条件求出细绳的拉力，
解答：解：以M为研究对象，设细绳与竖直方向的夹角为α，细绳拉力大小为T，则由平衡条件得：Tcosα=Mg
以O为支点，设杆长为L，PO间距离为l．根据力矩平衡条件得：mg?
=Nl+Tcosα?L
由以上两式得 mg?
=Nl+MgL
由于M、m、l、L均不变，则得N不变，即P对杆的支持力不变，则P处受到的压力不变．
当M运动到最低点，刚好使杆离开P时，此时P对轻杆的支持力为零，则有
mg?
=T
，
解得，T=50N
设M经过最低点的速度大小为v，则由牛顿第二定律得
T-Mg=M
解得v2=2.5
根据机械能守恒得；Mgy=
Mv2
解得y=0.125m
故答案为：不变，0.125
以O为支点，设杆长为L，PO间距离为l．根据力矩平衡条件得：mg?
| L |
| 2 |
由以上两式得 mg?
| L |
| 2 |
由于M、m、l、L均不变，则得N不变，即P对杆的支持力不变，则P处受到的压力不变．
当M运动到最低点，刚好使杆离开P时，此时P对轻杆的支持力为零，则有
mg?
| L |
| 2 |
| L |
| 2 |
解得，T=50N
设M经过最低点的速度大小为v，则由牛顿第二定律得
T-Mg=M
| v2 |
| R |
解得v2=2.5
根据机械能守恒得；Mgy=
| 1 |
| 2 |
解得y=0.125m
故答案为：不变，0.125
点评：本题是一道综合较强的题目，整合了共点力平衡、力矩平衡、牛顿第二定律和机械能守恒等多个力学知识，关键要把握物理规律，分析临界条件．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2009?上海二模）如图所示，一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送．斜面与传送带靠在一起连成一直线，与水平方向夹角θ，传送带以较大的恒定速率转动，传送方向向上，木板与传送带之间动摩擦因数为常数．已知木板放在斜面或者传送带上任意位置时，支持力均匀作用在木板底部．将木板静止放在传送带和光滑斜面之间某一位置，位于传送带部位的长度设为x，当x=L/4时，木板能保持静止．
（2009?上海二模）某电场中沿x方向上，电势φ与x方向的距离关系如图所示，假想有一个电子在其中仅受电场力作用下移动，则下列关于电场和电子能量说法正确的是（ ）
（2009?上海二模）如图所示，将斜面体固定在水平面上，其两个斜面光滑，斜面上放置一质量不计的柔软薄纸带．现将质量为mA的A物体和质量为mB的B物体轻放在纸带上．两物体可视为质点，物体初始位置及数据如图所示．
（2009?黄浦区二模）右图为ARJ21-700飞机在上海成功实现首飞的雄姿，它是中国首架自主研制、拥有完全自主知识产权的新型涡扇支线飞机．假定飞机的质量为m，以水平速度v0飞离跑道后逐渐上升，在此过程中水平速度保持不变，同时受到重力和竖直向上的恒定升力（该升力由其它力的合力提供，不含重力）．现测得当飞机从飞离地面开始算起，在水平方向的位移为s时，它的上升高度为h．求：