题目内容
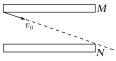
【题目】如图所示，在光滑水平面上有质量为m的小物块a以初速度v0水平向右运动，在小物块a左右两侧各放置完全相同的小物块b、c，小物块b、c上各固定一个轻弹簧，小物块b、c的质量均为km，其中k＝1、2、3…，弹簧始终处于弹性限度内．求：
(1)小物块a第一次与小物块c碰撞时，弹簧的最大弹性势能为多大？
(2)若小物块a至少能与小物块c碰撞2次，k的最小值为多少？
【答案】(1) 
(2)5
【解析】
(1)小物块a和c相互作用，两者速度相等时弹簧的弹性势能最大，对于小物块a和c，根据动量守恒定律有
mv0＝(m＋km)v
根据能量转化和守恒定律有
Epmax＝
(m＋km)v2
联立解得
Epmax＝
(2)设小物块a第一次离开小物块c时，小物块a和c的速度分别为v1、v2，对于小物块a和c根据动量守恒定律有
mv0＝mv1＋kmv2
根据机械能守恒定律有
联立解得，小物块a的速度为
v1＝
v0
小物块c的速度为
v2＝
v0
小物块a离开c后与小物块b作用，当小物块a离开b时，小物块a和小物块b的速度分别为v′1、v′2，对于小物块a和b，根据动量守恒定律有
mv1＝mv′1＋kmv′2
根据机械能守恒定律有
联立解得
v′1＝
v0
若小物块a和c至少碰撞2次，则有v′1＞v2，由数学知识可得k2－4k－1＞0，解得
k＞2＋
而k＝1、2、3．．．．．．
故
kmin＝5
练习册系列答案
灵星计算小达人系列答案
相关题目
