题目内容
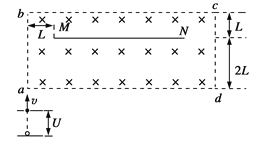
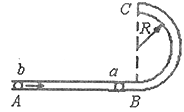
【题目】某机械装置的竖直切面如图所示,装置由内壁光滑的圆管构成,其中AB部分水平,BC部分是内径为R的半圆,且圆管半径远小于R。由于某种原因,一质量为m的小球a留在了水平管内,现用一个质量也为m的小球b“冲撞”小球a,小球a恰好到达圆管最高点C.已知两小球发生弹性正碰,两小球直径略小于圆管直径,重力加速度为g.则小球b的入射速度大小为____,小球b对小球a的冲量大小为_____。
【答案】 ![]()
![]()
【解析】小球a恰好到达圆管最高点C,速度为零,即:vc=0
小球a从A到C,由机械能守恒得: ![]() mva2=2mgR
mva2=2mgR
解得:va=2![]()
对于碰撞过程,取向右为正方向,由动量守恒定律和机械能守恒定律得:
mv0=mvb+mva。![]() mv02=
mv02=![]() mvb2+
mvb2+![]() mva2。
mva2。
解得:v0=va=2![]() 。
。
对a球,由动量定理得:
I=mva-0=2m![]() 。
。
点睛:对于小球在管子里的运动情形与轻杆模型类似,关键抓住临界情况:小球恰好到最高点时速度为零。对于弹性碰撞,要抓住两大守恒:动量守恒和机械能守恒。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目