题目内容
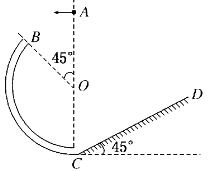
【题目】如图所示，BC为半径等于
m竖直放置的光滑细圆管，O为细圆管的圆心，在圆管的末端C连接倾斜角为45°、动摩擦因数μ＝0．6的足够长粗糙斜面，一质量为m＝0．5kg的小球从O点正上方某处A点以v0水平抛出，恰好能垂直OB从B点进入细圆管，小球从进入圆管开始受到始终竖直向上的力F＝5N的作用，当小球运动到圆管的末端C时作用力F立即消失，小球能平滑地冲上粗糙斜面．（g＝10m/s2）求：
（1）小球从O点的正上方某处A点水平抛出的初速度v0为多少？OA的距离为多少？
（2）小球在圆管中运动时对圆管的压力是多少？
（3）小球在CD斜面上运动的最大位移是多少？
【答案】（1）2m/s；0．6m（2）
（3）
【解析】
试题分析：（1）小球从A运动到B为平抛运动,有: 
在B点,有: 
联立以上两式解得:v0=2m/s t=0．2s
AB竖直方向的距离为: 
B竖直方向的距离为: 
, 
（2）在B点据平抛运动的速度规律有：
小球在管中的受力分析为三个力：由于重力与外加的力F平衡，故小球所受的合力仅为管的外轨对它的压力，得小球在管中做匀速圆周运动，由圆周运动的规律得细管对小球的作用力为：
根据牛顿第三定律得小球对细管的压力为： 
（3）在CD上滑行到最高点过程中,根据牛顿第二定律得: mgsin45°+μmgcos45°=ma
解得: 
根据速度位移关系式,得: 
练习册系列答案
相关题目
