题目内容
(2008?武汉一模)直立轻弹簧的下端与水平地面上质量为M=0.20kg的甲木块与连接,轻弹簧上端静止于A点(如图1),再将质量也为M=0.20kg乙木块与弹簧的上端连接,当甲、乙及弹簧均处于静止状态时,弹簧上端位于B点(如图2).现向下用力压乙,当弹簧上端下降到C点时将弹簧锁定,C、A两点间的距离为△l=6.0cm.一个质量为m=0.10kg的小球丙从距离乙正上方h=0.45m处自由落下(如图3),当丙与乙刚接触时,弹簧立即被解除锁定,之后,丙与乙发生弹性碰撞(碰撞时间极短),碰撞后取走小球丙,当甲第一次刚离开地面时乙的速度为v=2.0m/s.求从弹簧被解除锁定至甲第一次刚离开地面时,弹簧弹性势能的改变量.(g=10m/s2)


分析:根据丙做自由落体运动求出碰撞前丙的速度,以乙和丙组成的系统为研究对象,系统动量守恒,根据动量守恒定律和机械能守恒定律列方程求解.
对乙研究,碰后,乙立即以2m/s的速度从C点向下运动,从此时起直到甲第一次刚离开地面前,乙在自身重力和弹簧弹力的共同作用下以B点为平衡位置做简谐运动.由于甲第一次刚离开地面时乙的速度为v=2.0m/s,v和v2等大反向.根据简谐振动的对称性和胡克定律列方程.
根据功能关系,系统重力势能的增加量△E重等于弹性势能的减少量△E弹列方程求解.
对乙研究,碰后,乙立即以2m/s的速度从C点向下运动,从此时起直到甲第一次刚离开地面前,乙在自身重力和弹簧弹力的共同作用下以B点为平衡位置做简谐运动.由于甲第一次刚离开地面时乙的速度为v=2.0m/s,v和v2等大反向.根据简谐振动的对称性和胡克定律列方程.
根据功能关系,系统重力势能的增加量△E重等于弹性势能的减少量△E弹列方程求解.
解答:解:设丙与乙碰前瞬间速度为υ0,由机械能守恒有v0=
=3.0m/s
解除锁定后,乙与丙发生弹性碰撞,设碰后乙、丙的速度分别为v乙、v丙,
根据动量守恒定律mv0=mv丙+Mv乙
根据动能守恒
m
=
M
+
m
解得:
碰后,乙立即以v乙=2.0m/s的速度从C点向下运动,从此时起直到甲第一次刚离开地面的时间内,乙以B点为平衡位置做简谐运动(如图).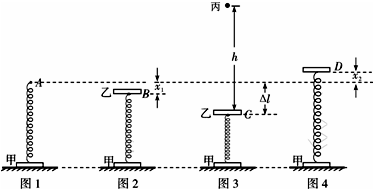
当乙第一次回到平衡位置B时,弹簧相对原长的压缩量(图2)x1=
当甲第一次刚离开地面时,弹簧相对原长的伸长量(图4)x2=
由于甲第一次刚离开地面时乙的速度为v=2.0m/s,v和v乙等大反向,所以根据简谐振动的对称性可知 x1+x2=△l-x1
故 x1=x2=
=2.0cm
从碰撞结束至甲第一次刚离开地面时,对于乙和弹簧组成的系统,动能变化量为△EK=
Mv2-
M
=0
根据功能关系,系统重力势能的增加量△E重等于弹性势能的减少量△E弹=△E重
重力势能的增加量△E重=Mg(x2+△l)
所以弹簧弹性势能的减少量为△E弹=Mg(x2+△l)=0.16J
答:弹簧弹性势能的改变量是0.16J
| 2gh |
解除锁定后,乙与丙发生弹性碰撞,设碰后乙、丙的速度分别为v乙、v丙,
根据动量守恒定律mv0=mv丙+Mv乙
根据动能守恒
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 乙 |
| 1 |
| 2 |
| v | 2 丙 |
解得:
|
碰后,乙立即以v乙=2.0m/s的速度从C点向下运动,从此时起直到甲第一次刚离开地面的时间内,乙以B点为平衡位置做简谐运动(如图).

当乙第一次回到平衡位置B时,弹簧相对原长的压缩量(图2)x1=
| Mg |
| k |
当甲第一次刚离开地面时,弹簧相对原长的伸长量(图4)x2=
| Mg |
| k |
由于甲第一次刚离开地面时乙的速度为v=2.0m/s,v和v乙等大反向,所以根据简谐振动的对称性可知 x1+x2=△l-x1
故 x1=x2=
| △l |
| 3 |
从碰撞结束至甲第一次刚离开地面时,对于乙和弹簧组成的系统,动能变化量为△EK=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 乙 |
根据功能关系,系统重力势能的增加量△E重等于弹性势能的减少量△E弹=△E重
重力势能的增加量△E重=Mg(x2+△l)
所以弹簧弹性势能的减少量为△E弹=Mg(x2+△l)=0.16J
答:弹簧弹性势能的改变量是0.16J
点评:此题要用动量守恒定律和机械能守恒定律联合列方程求解,既要分析动量是否守恒,又要分析机械能是否守恒,同时还要熟练掌握简谐运动的知识.此题对能力要求较高,属于难题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 (2008?武汉一模)如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)、一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )
(2008?武汉一模)如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)、一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )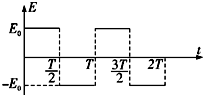 (2008?武汉一模)在竖直方向的电场中某处固定一个质量为m、电荷量为+q的小球,场强E的变化规律如图所示,以竖直向上为场强的正方向,E0=2mg/q.t(0≤t<T)时刻释放小球,在t~t+T时间内合力的冲量大小为( )
(2008?武汉一模)在竖直方向的电场中某处固定一个质量为m、电荷量为+q的小球,场强E的变化规律如图所示,以竖直向上为场强的正方向,E0=2mg/q.t(0≤t<T)时刻释放小球,在t~t+T时间内合力的冲量大小为( ) ):绕制螺线管金属丝的电阻率ρ=5.0×10-7Ω?m,电阻RL约为100Ω
):绕制螺线管金属丝的电阻率ρ=5.0×10-7Ω?m,电阻RL约为100Ω
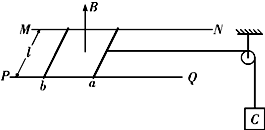 (2008?武汉一模)如图所示,间距为l、电阻不计的两根平行金属导轨MN、PQ(足够长)被固定在同一水平面内,质量均为m、电阻均为R的两根相同导体棒a、b垂直于导轨放在导轨上,一根轻绳绕过定滑轮后沿两金属导轨的中线与a棒连接,其下端悬挂一个质量为M的物体C,整个装置放在方向竖直向上、磁感应强度大小为B的匀强磁场中.开始时使a、b、C都处于静止状态,现释放C,经过时间t,C的速度为υ1、b的速度为υ2.不计一切摩擦,两棒始终与导轨接触良好,重力加速度为g,求:
(2008?武汉一模)如图所示,间距为l、电阻不计的两根平行金属导轨MN、PQ(足够长)被固定在同一水平面内,质量均为m、电阻均为R的两根相同导体棒a、b垂直于导轨放在导轨上,一根轻绳绕过定滑轮后沿两金属导轨的中线与a棒连接,其下端悬挂一个质量为M的物体C,整个装置放在方向竖直向上、磁感应强度大小为B的匀强磁场中.开始时使a、b、C都处于静止状态,现释放C,经过时间t,C的速度为υ1、b的速度为υ2.不计一切摩擦,两棒始终与导轨接触良好,重力加速度为g,求: