题目内容
5. 如图所示,倾角θ=37°的光滑且足够长的斜面固定在水平面上,在斜面顶端固定一个轮半径和质量不计的光滑定滑轮 D,质量均为m=1kg的体A和B用一劲度系数Bk=240N/m的轻弹簧连接,物体B被位于斜面底端且垂直于斜面P的挡板P挡住.用一不可伸长的轻绳使物体A跨过定滑轮与质量为M的小环C连接,小环C穿过竖直固定的光滑均匀细杆,当整个系统静止时,环C位于Q处,绳与细杆的夹角α=53°,且物体B对挡板P的压力恰好为零.图中SD水平且长度为d=0.2m,位置R与位置Q关于位置S对称,轻弹簧和定滑轮右侧的绳均与斜面平行.现让环C从位置R由静止释放,sin37°=0.6,cos37°=0.8,g取10m/s2.求:
如图所示,倾角θ=37°的光滑且足够长的斜面固定在水平面上,在斜面顶端固定一个轮半径和质量不计的光滑定滑轮 D,质量均为m=1kg的体A和B用一劲度系数Bk=240N/m的轻弹簧连接,物体B被位于斜面底端且垂直于斜面P的挡板P挡住.用一不可伸长的轻绳使物体A跨过定滑轮与质量为M的小环C连接,小环C穿过竖直固定的光滑均匀细杆,当整个系统静止时,环C位于Q处,绳与细杆的夹角α=53°,且物体B对挡板P的压力恰好为零.图中SD水平且长度为d=0.2m,位置R与位置Q关于位置S对称,轻弹簧和定滑轮右侧的绳均与斜面平行.现让环C从位置R由静止释放,sin37°=0.6,cos37°=0.8,g取10m/s2.求:(1)小环C的质量M;
(2)小环C通过位置S时的动能Ek及环从位置R运动到位置S的过程中轻绳对环做的功WT;
(3)小环C运动到位置Q的速率v.
分析 (1)该题中,共有ABC三个物体与弹簧组成一个系统,受力的物体比较多,可以先以AB组成的整体为研究对象,求出绳子的拉力,然后以C为研究对象进行受力分析,即可求出C的质量;
(2)由几何关系求出绳子RD段的长度,再以B为研究对象,求出弹簧的伸长量,以及后来的压缩量,最后根据机械能守恒定律求出C的速度、动能;由动能定理求出轻绳对环做的功WT;
(3)由机械能守恒定律即可求出C的速度.
解答 解:(1)先以AB组成的整体为研究对象,AB系统受到重力.支持力和绳子的拉力处于平衡状态,则绳子的拉力为:
T=2mgsinθ=2×10×sin37°=12N
以C为研究对象,则C受到重力、绳子的拉力和杆的弹力处于平衡状态,如图,则:
T•cos53°=Mg
代入数据得:M=0.72kg
(2)考虑到本题中弹簧有不同的形变量,所以需要先计算不同情况下弹簧的形变量,然后判断出是否需要使用弹簧的弹性势能的表达式.
所以需要先计算出弹簧开始时的形变量.
由题意,开始时B恰好对挡板没有压力,所以B受到重力、支持力和弹簧的拉力,弹簧处于伸长状态;产生B沿斜面方向的受力:
F1=mgsinθ=1×10×sin37°=6N
弹簧的伸长量:$△{x}_{1}=\frac{{F}_{1}}{k}=\frac{6}{240}=0.025$m
由题图中的几何关系可知:$\overline{RD}=\overline{QD}=\frac{\overline{SD}}{sinα}=\frac{d}{sin53°}=\frac{0.2}{0.8}=0.25$m
所以C由R点运动到S点的过程中,弹簧将缩短:$x=\overline{RD}-\overline{SD}=0.25-0.20=0.05$m>0.025m
可知弹簧将由开始时的伸长状态变成压缩状态,压缩量:△x2=x-△x1=0.05-0.025=0.025m=△x1
由于弹簧的压缩量等于弹簧开始时的伸长量,所以当C运动到S点时,弹簧的弹性势能与开始时的弹性势能是相等的.而A下降的距离等于弹簧缩短的距离x,即0.05m.
在C从R点运动到S点的过程中,C受到的重力、A受到的重力对A与C组成的系统 做功.当C到达S点时,C沿绳子方向的分速度是0,所以A的速度是0,A与C减小的重力势能转化为C的动能,由机械能守恒定律得:
$Mg•\overline{RS}+mg•x•sinθ=\frac{1}{2}M{v}_{1}^{2}$
代入数据求得环C的动能:${E}_{k}=\frac{1}{2}M{v}_{1}^{2}=1.38$J
环下降的过程中重力和绳子的拉力对环做功,由动能定理得:$Mg•\overline{RS}+{W}_{T}={E}_{k}$
代入数据,得:WT=0.3J
(3)结合第二步的分析可知,当环到达Q点时,由于$\overline{RD}=\overline{QD}$,所以,物体A恰好又回到了开始时的位置,弹簧的长度又回到了最初的长度,所以环从R到S的过程中,只有环的重力势能减小,其他的物体的势能保持不变!
对环在Q点的速度进行分解如下图,则: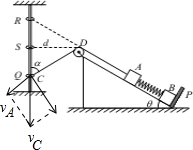
由图可知,物体A上升的速度即沿绳子方向的速度,是环C的一个分速度,它们之间的关系:
$\frac{{v}_{A}}{{v}_{Q}}=cosα=cos53°=0.6$
所以:vA=0.6vQ
由功能关系:$Mg\overline{RQ}=\frac{1}{2}M{v}_{Q}^{2}+\frac{1}{2}m{v}_{A}^{2}$
代入数据解得:vQ=2m/s
答:(1)小环C的质量 是0.72kg;
(2)小环C通过位置S时的动能Ek是1.38J,环从位置R运动到位置S的过程中轻绳对环做的功是0.3J;
(3)小环C运动到位置Q的速率是2m/s.
点评 本题考查动能定理以及功能关系的应用,解题的关键在于第二问,要注意在解答的过程中一定要先得出弹簧的弹性势能没有变化的结论,否则解答的过程不能算是完整的.

 阅读快车系列答案
阅读快车系列答案
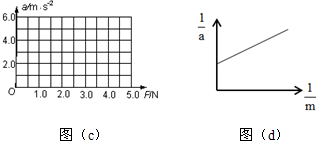
(1)在图(c)坐标纸上作出小车加速度a和拉力F的关系图线;
(2)从所得图线分析该实验小组在操作过程中的不当之处是倾角过大或平衡摩擦力过度;
(3)如果实验时,在小车和重物之间接一个不计质量的微型力传感器来测量绳子的拉力大小,如图(b)所示.要满足小车质量M远大于重物的质量m是不必要的.(填“必要”或“不必要”)
| a/ms-2 | 2.01 | 2.98 | 4.02 | 6.00 |
| F/N | 1.00 | 2.00 | 3.00 | 5.00 |
| A. | 电场和电场线都是人为构想出来的,实际上不存在 | |
| B. | 同一电场中,电场线越密集的地方电场强度越大;越稀疏的地方电场越弱 | |
| C. | 在电场中,电场线通过的地方场强不为零,不画电场线的地方电场强度为零 | |
| D. | 电荷之间的相互作用是通过电场来完成的,场是一种物质 |
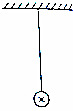 有一根质量为m、长度为d的通有水平向里的电流I的导体棒,被长度为L的轻质绝缘细线悬挂在天花板上,在此空间加上竖直向下的匀强磁场,磁场的磁感应强度大小为B=$\frac{\sqrt{3}mg}{3Id}$,若保持导体棒中的电流I始终不变,则( )
有一根质量为m、长度为d的通有水平向里的电流I的导体棒,被长度为L的轻质绝缘细线悬挂在天花板上,在此空间加上竖直向下的匀强磁场,磁场的磁感应强度大小为B=$\frac{\sqrt{3}mg}{3Id}$,若保持导体棒中的电流I始终不变,则( )| A. | 细线偏离竖直方向的夹角最大为30° | |
| B. | 细线偏离竖直方向的夹角最大为60° | |
| C. | 在导体棒摆动过程中细线上拉力最大为2($\sqrt{3}$-1)mg | |
| D. | 在导体棒摆动过程中细线上拉力最大为$\frac{(12+\sqrt{3})mg}{6}$ |
| A. | 1.875×106 | B. | 3.75×106 | C. | 1.875×105 | D. | 3.75×105 |
| A. | 两表指针偏角相同?? | |
| B. | 两表指针都不偏转 | |
| C. | 伏特表指针有偏转,安培表指针几乎不偏转 | |
| D. | 安培表指针有偏转,伏特表指针几乎不偏转 |
 (1)如图1所示:小车沿倾角为θ=37°的斜面匀速滑下,在小车上有一质量为M=1Kg的木块和小车保持相对静止,小车上表面和斜面平行.求小车下滑时木块所受的摩擦力和弹力?
(1)如图1所示:小车沿倾角为θ=37°的斜面匀速滑下,在小车上有一质量为M=1Kg的木块和小车保持相对静止,小车上表面和斜面平行.求小车下滑时木块所受的摩擦力和弹力? 如图所示,有一内表面光滑的金属盒,底面长为L=1.2m,质量为m1=1kg,放在水平面上,与水平面间的动摩擦因数为μ=0.2,在盒内最右端放一半径为r=0.1m的光滑金属球,质量为m2=1kg,现在盒的左端,给盒一个初速度v=3m/s(盒壁厚度,球与盒发生碰撞的时间和能量损失均忽略不计,g取10m/s2)求:
如图所示,有一内表面光滑的金属盒,底面长为L=1.2m,质量为m1=1kg,放在水平面上,与水平面间的动摩擦因数为μ=0.2,在盒内最右端放一半径为r=0.1m的光滑金属球,质量为m2=1kg,现在盒的左端,给盒一个初速度v=3m/s(盒壁厚度,球与盒发生碰撞的时间和能量损失均忽略不计,g取10m/s2)求: