题目内容
如图8-7-9所示，在固定的水平光滑横杆上，套着一个轻质小环，一条线的一端连于轻环，另一端系一小球.与球的质量相比，轻环和线的质量可忽略不计.开始时，将系球的线绷直并拉到与横杆平行的位置，释放小球，线与横杆的夹角θ逐渐增大.试问：θ由0°增大到90°的过程中，小球的速度的水平分量是怎样变化的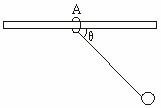
图 8-7-9
A.一直增大 B.先增大后减小
C.始终为零 D.以上说法都不对
解析：轻环和小球组成的系统在水平方向上不受力，动量守恒，应有m1v1′+m2v2′=0,因轻环质量m1可忽略不计，故其动量m1v1也可忽略不计，则由上式得小球动量m2v2′=0, v2′=0,即小球水平分速度v2′=0.
答案：C
要使R2在保温状态时的功率为加热状态时的1/8，R1/R2应为（2
－1）∶1
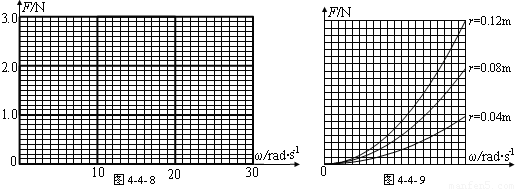
一物理兴趣小组利用学校实验室的数字实验系统探究物体作圆周运动时向心力与角速度、半径的关系.
（1）首先，他们让一砝码做半径r为0.08m的圆周运动，数字实验系统通过测量和计算得到若干组向心力F和对应的角速度ω，如下表．请你根据表中的数据在图4-4-8所示的坐标上绘出F-ω的关系图像.
|
实验序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
F/N |
2.42 |
1.90 |
1.43 |
0.97 |
0.76 |
0.50 |
0.23 |
0.06 |
|
ω/rad·s-1 |
28.8 |
25.7 |
22.0 |
18.0 |
15.9 |
13.0 |
8.5 |
4.3 |
（2）通过对图像的观察，兴趣小组的同学猜测F与ω2成正比．你认为，可以通过进一步的转换，通过绘出____________关系图像来确定他们的猜测是否正确．
（3）在证实了F∝ω2之后，他们将砝码做圆周运动的半径r再分别调整为0.04m、0.12m，又得到了两条F-ω图像，他们将三次实验得到的图像放在一个坐标系中，如图4-4-9所示．通过对三条图像的比较、分析、讨论，他们得出F∝ r的结论，你认为他们的依据是 _____________________________ ．
（4）通过上述实验，他们得出：做圆周运动的物体受到的向心力F与角速度ω、半径r的数学关系式是F=kω2r，其中比例系数k的大小为__________，单位是________．
