题目内容
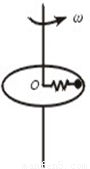
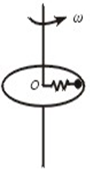 如图所示,原长为L的轻质弹簧,劲度系数为k,一端系在圆盘的中心O,另一端系一质量为m的金属球,不计摩擦,当盘和球一起旋转时弹簧伸长量为△L,则盘旋转的向心加速度为
如图所示,原长为L的轻质弹簧,劲度系数为k,一端系在圆盘的中心O,另一端系一质量为m的金属球,不计摩擦,当盘和球一起旋转时弹簧伸长量为△L,则盘旋转的向心加速度为| k△L |
| m |
| k△L |
| m |
|
|
分析:小球做圆周运动所需的向心力由弹簧的拉力提供,根据牛顿第二定律求出物体的向心加速度,以及角速度.
解答:解:弹簧的弹力F=k△L,则向心力大小为k△L,向心加速度a=
.
根据a=rω2=(L+△L)ω2,则ω=
故答案为:
,
.
| k△L |
| m |
根据a=rω2=(L+△L)ω2,则ω=
|
故答案为:
| k△L |
| m |
|
点评:解决本题的关键知道向心力的来源,根据牛顿第二定律求加速度,以及知道向心加速度与角速度的关系.

练习册系列答案
相关题目
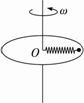

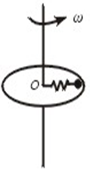 如图所示,原长为L的轻质弹簧,劲度系数为k,一端系在圆盘的中心O,另一端系一质量为m的金属球,不计摩擦,当盘和球一起旋转时弹簧伸长量为△L,则盘旋转的向心加速度为________,角速度为________.
如图所示,原长为L的轻质弹簧,劲度系数为k,一端系在圆盘的中心O,另一端系一质量为m的金属球,不计摩擦,当盘和球一起旋转时弹簧伸长量为△L,则盘旋转的向心加速度为________,角速度为________.