题目内容
【题目】如图所示,BCD为固定在竖直平面内的半径为r=10m的圆弧形光滑绝缘轨道,O为圆心,OC竖直,OD水平,OB与OC间夹角为53°,整个空间分布着范围足够大的竖直向下的匀强电场。从A点以初速v0=9m/s沿AO方向水平抛出质量m=0.1kg的小球(小球可视为质点),小球带正电荷q=+0.01C,小球恰好从B点沿垂直于OB的方向进入圆弧轨道。不计空气阻力。求:
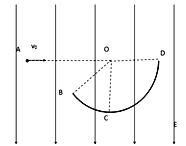
(1)A、B间的水平距离L
(2)小球过C点时对轨道的压力的大小FN
【答案】(1)9m (2)4.41N
【解析】
根据平行四边形定则求出B点的竖直分速度,根据几何关系求出竖直位移,抓住竖直方向上做初速度为零的匀加速直线运动,结合运动学公式求出运动的时间,从而求出A、B间的水平距离。
(1)从A到B,根据平行四边形定则知:vBy=v0tan53°
根据速度时间公式:vBy=at
下落距离为:y=rcos53°
根据位移时间公式:y=![]() at2
at2
联立代入数据解得:t=1s a=12m/s2
则A、B间的水平距离:L=v0t=9×1m=9m。
(2)从A到C,根据动能定理得:mar=![]() -
-![]()
在C点,根据牛顿第二定律可得:FN-ma=![]()
代入数据解得:FN=4.41N

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目