题目内容
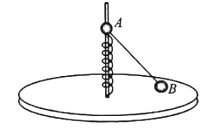
【题目】如图所示,一根左侧弯成![]() 圆弧的光滑细管固定在竖直平面内,圆弧半径R=0.5m,水平部分足够长。初始时,一根质量m=1kg、与管道
圆弧的光滑细管固定在竖直平面内,圆弧半径R=0.5m,水平部分足够长。初始时,一根质量m=1kg、与管道![]() 圆弧部分等长的柔软匀质绳在水平拉力F0作用下静止在管道中。现将绳子缓慢全部拉入水平管道内,需要拉力F0做功W=1. 82J。g取10m/s2,π取3.14。求:
圆弧部分等长的柔软匀质绳在水平拉力F0作用下静止在管道中。现将绳子缓慢全部拉入水平管道内,需要拉力F0做功W=1. 82J。g取10m/s2,π取3.14。求:
(1)绳子的重心升高了多少?
(2)若在图示位置撤去拉力,绳子沿细管下落,当其上端离开管道瞬间速度多少?
(3)若在缓慢拉动绳子进入水平管道的很短距离ΔL内,可认为水平拉力F0保持不变,拉力F0做功等于绳子机械能增加量,则F0的大小为多少?

【答案】(1)0.182m(2)1.19m/s(3)6.37N
【解析】
(1)绳子缓慢拉入水平管道重心升高h
由动能定理:
W+WG=0
W=mgh
h=0.182m
(2)由动能定理(或机械能守恒)
WG=ΔEK
![]()
v=1.19m/s
(3)拉力做功,效果等同于底端长ΔL的绳子被拉到水平管内
由题意(或动能定理)
![]()
其中
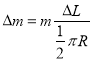
![]() =6.37N
=6.37N

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目